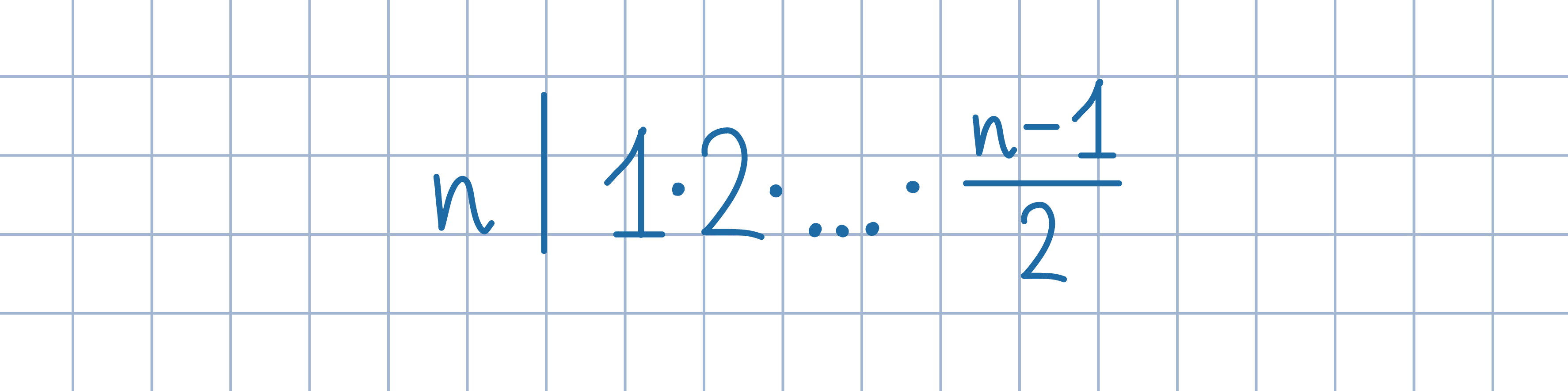mat edukacja
Uczymy się razem
Konkursy
Konkursy
matematyczne OMJ Olimpiada
Matematyczna
Juniorów OM 2 etap Olimpiada
Matematyczna
2 etap
matematyczne OMJ Olimpiada
Matematyczna
Juniorów OM 2 etap Olimpiada
Matematyczna
2 etap
Przed 2 etapem Olimpiady Matematycznej
Zadania
Zadanie 3–41.
Na płaszczyźnie dany jest wielokąt, którego wszystkie wierzchołki mają obie współrzędne całkowite i którego wszystkie boki mają całkowite długości. Dowieść, że obwód tego wielokąta jest liczbą parzystą.
Uzasadnij, że jeśli boki trójkąta prostokątnego mają całkowite długości, to parzystość przeciwprostokątnej jest taka sama jak parzystość sumy przyprostokątnych. Wykorzystując tę własność, sprowadź zadanie do przypadku, w którym każdy bok jest ułożony pionowo lub poziomo.
Zadanie 3–40.
Na szachownicy o wymiarach n na 1 należy ustawić pewną liczbę pionków w taki sposób, aby żadne dwa pionki nie stały na sąsiadujących polach (na każde pole stawiamy co najwyżej jeden pionek). Na ile sposobów można to zrobić?
Odp. Szukana liczba to F_(n+2), gdzie F_n jest ciągiem Fibonacciego, określonym wzorem
rekurencyjnym: F_0=0, F_1=1, F_(n+2)=F_(n+1)+F_n.
Uzasadnij, że liczba ułożeń pionków spełnia powyższy warunek rekurencyjny definiujący ciąg Fibonacciego.
Zadanie 3–39.
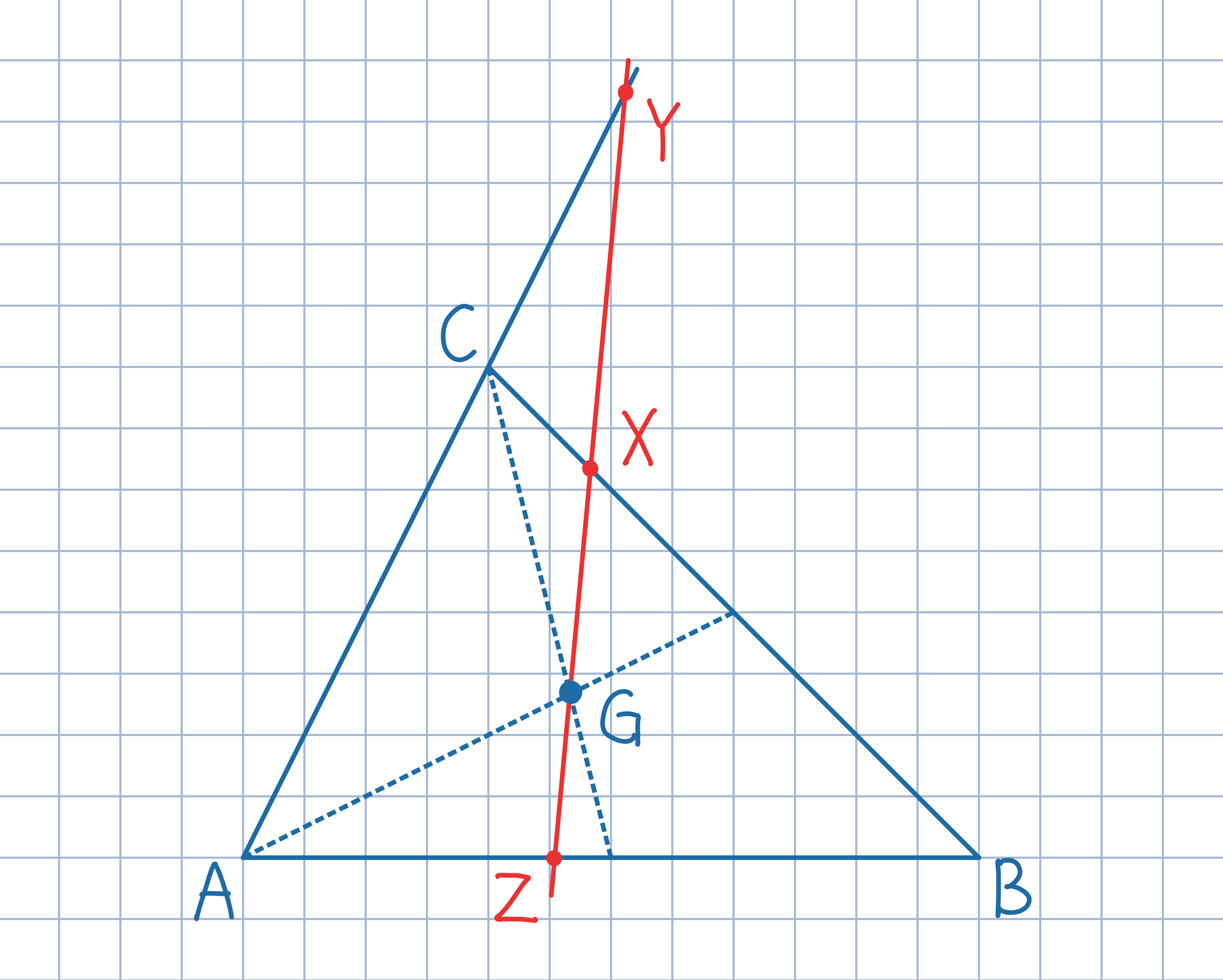
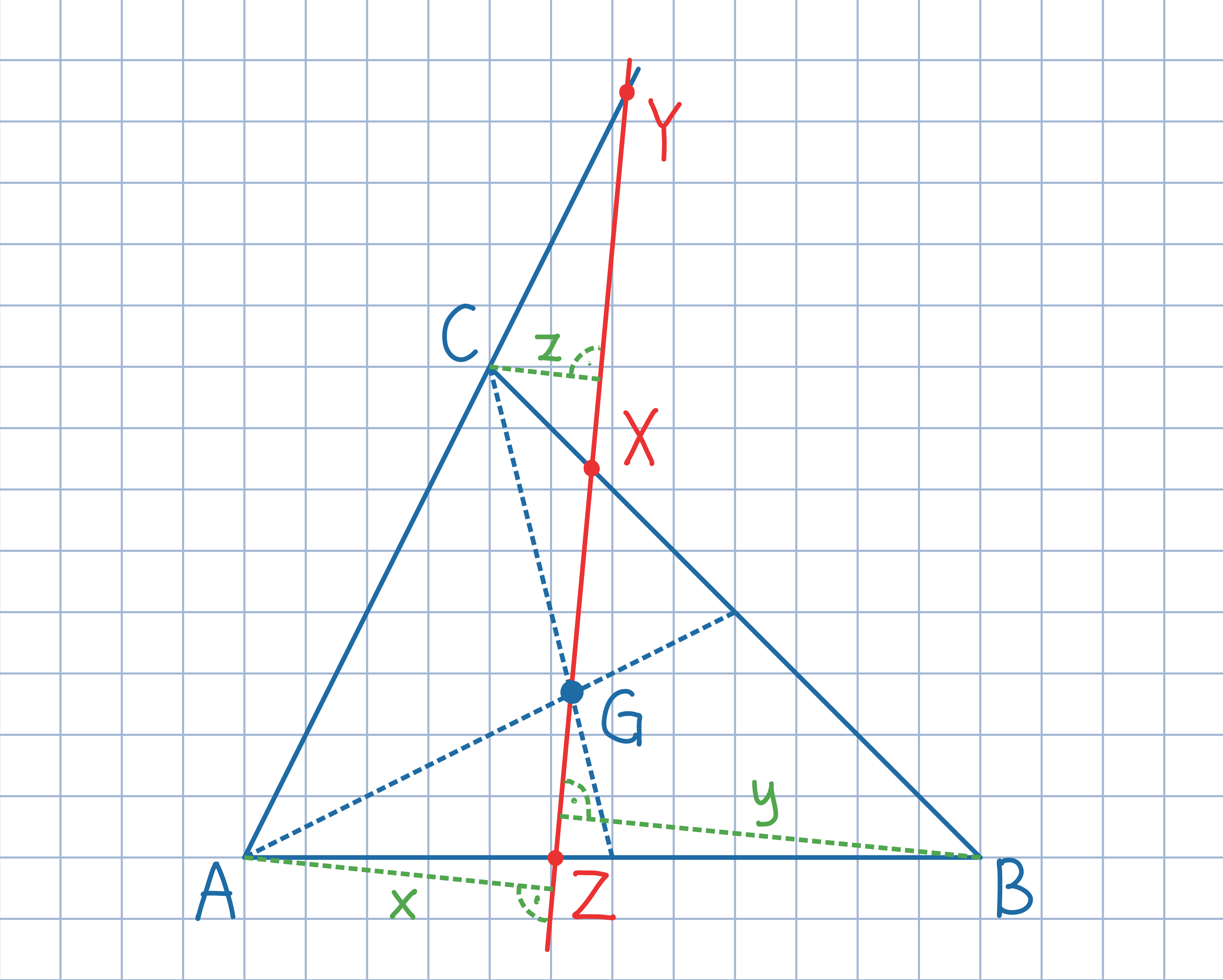
Punkt G jest środkiem ciężkości trójkąta ABC. Prosta przechodząca przez punkt G przecina proste BC, CA, AB odpowiednio w punktach X, Y, Z, przy czym punkty X, Y leżą po tej samej stronie punktu G. Wykazać, że 1/GX+1/GY=1/GZ.
Oznacz przez x, y, z odległości odpowiednio punktów A, B, C od danej prostej. Zauważ, że pole trójkąta ABG jest równe (x+y)GZ/2. Wyznacz w podobny sposób pola trójkątów BCG oraz CAG.
Zadanie 3–38.
Dla każdej dodatniej liczby całkowitej n wyznacz resztę z dzielenia przez n+1 liczby 1∙1!+2∙2!+...+n∙n!.
Odp. n.
Zauważ, że n∙n!=(n+1)!-n!.
Zadanie 3–37.
Wyznacz wszystkie liczby nieparzyste n>2, dla których liczba 1∙2∙...∙((n-1)/2) jest podzielna przez n.
Odp. n jest dowolną liczbą nieparzystą złożoną większą od 9.
Uzasadnij, że jeśli n=ab, gdzie a, b są różnymi liczbami naturalnymi większymi od 1,
to liczby a, b są mniejsze od (n-1)/2. Jeśli z kolei n=p^2, gdzie p jest liczbą naturalną,
to 2p<(n-1)/2 dla p>3.
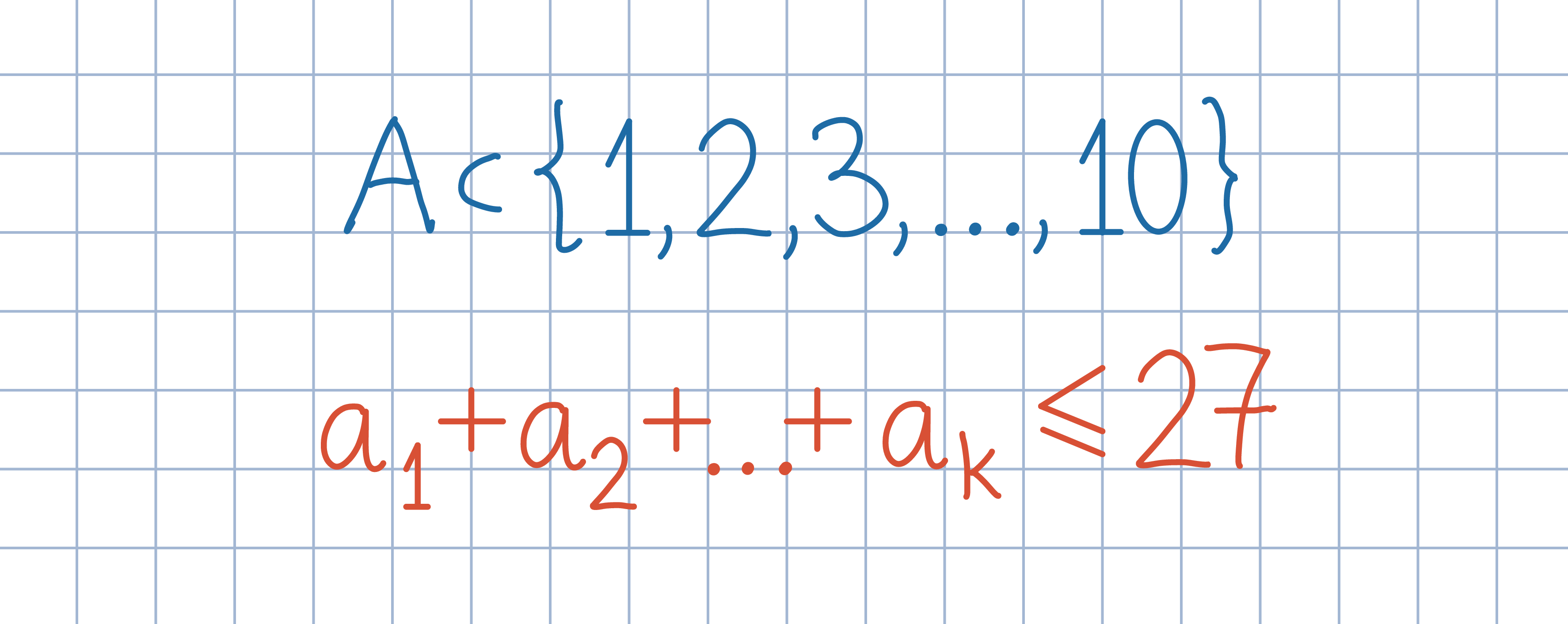 Odp.: 511.
Odp.: 511.Uzasadnij, że suma elementów pewnego (być może pustego) podzbioru nie przekracza 27 wtedy i tylko wtedy, gdy suma elementów dopełnienia tego zbioru jest większa od 27.
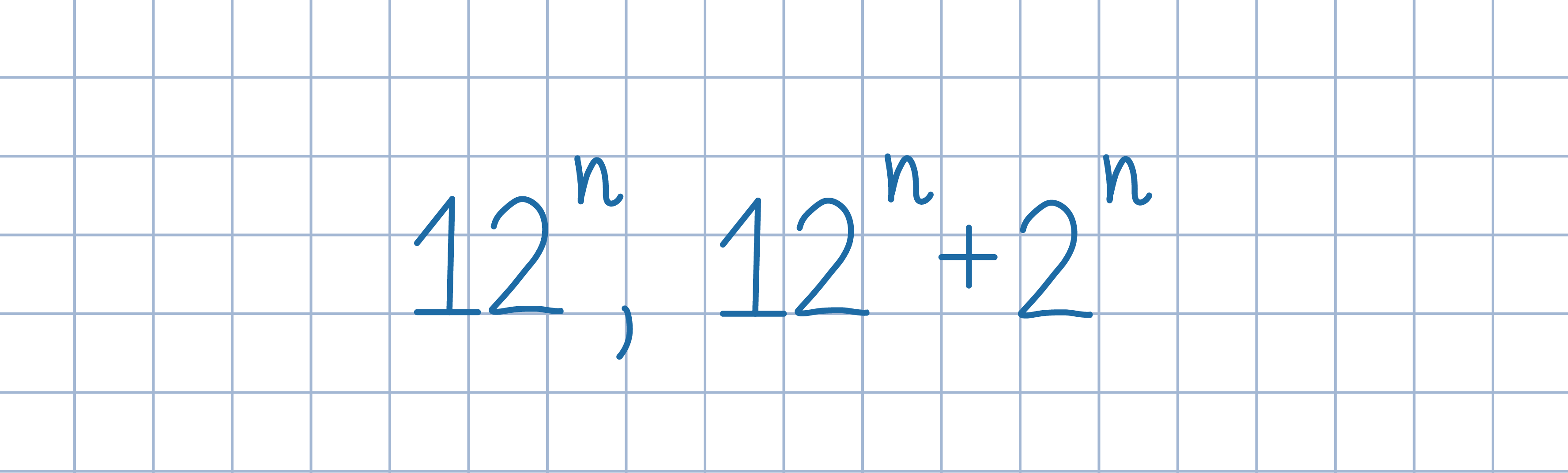 Gdyby liczby 12^n oraz 12^n+2^n miały różną liczbę cyfr, to wtedy
Gdyby liczby 12^n oraz 12^n+2^n miały różną liczbę cyfr, to wtedy
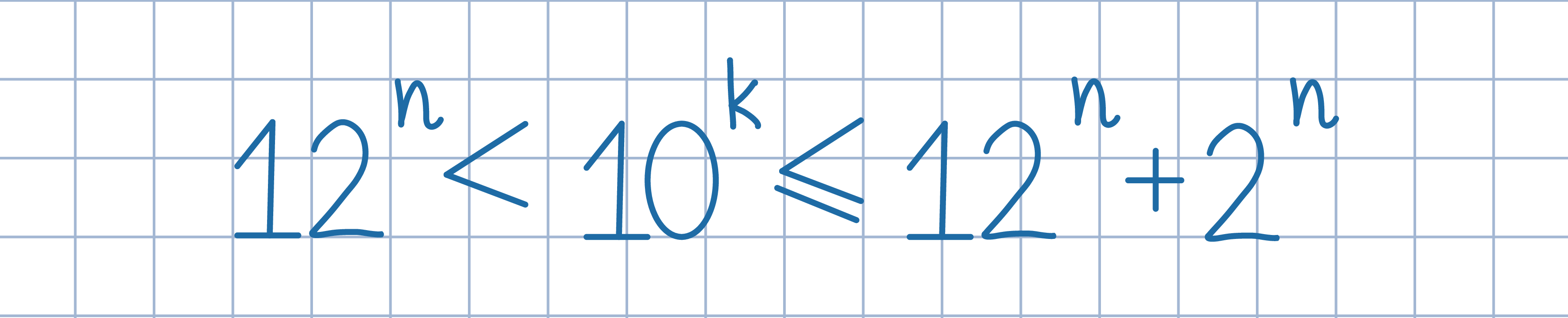
 Uzasadnij najpierw, że promień r okręgu wpisanego w trójkąt prostokątny
wyraża się wzorem r=(a+b-c)/2, gdzie a, b są przyprostokątnymi, a c przeciwprostokątną.
Następnie wykaż, że suma promieni okręgów czerwonych (a także zielonych)
nie zmienia się, gdy jeden z kwadratów przesuwamy (bez obracania).
Uzasadnij najpierw, że promień r okręgu wpisanego w trójkąt prostokątny
wyraża się wzorem r=(a+b-c)/2, gdzie a, b są przyprostokątnymi, a c przeciwprostokątną.
Następnie wykaż, że suma promieni okręgów czerwonych (a także zielonych)
nie zmienia się, gdy jeden z kwadratów przesuwamy (bez obracania).
 Podziel osoby na dwie grupy w taki sposób, aby łączna liczba znajomości pomiędzy obiema grupami była największa. Uzasadnij, że taki podział
spełnia warunki zadania.
Podziel osoby na dwie grupy w taki sposób, aby łączna liczba znajomości pomiędzy obiema grupami była największa. Uzasadnij, że taki podział
spełnia warunki zadania.
 Wykorzystaj nierówność Cauchy'ego-Schwarza dla odpowiednio dobranych liczb.
Wykorzystaj nierówność Cauchy'ego-Schwarza dla odpowiednio dobranych liczb.
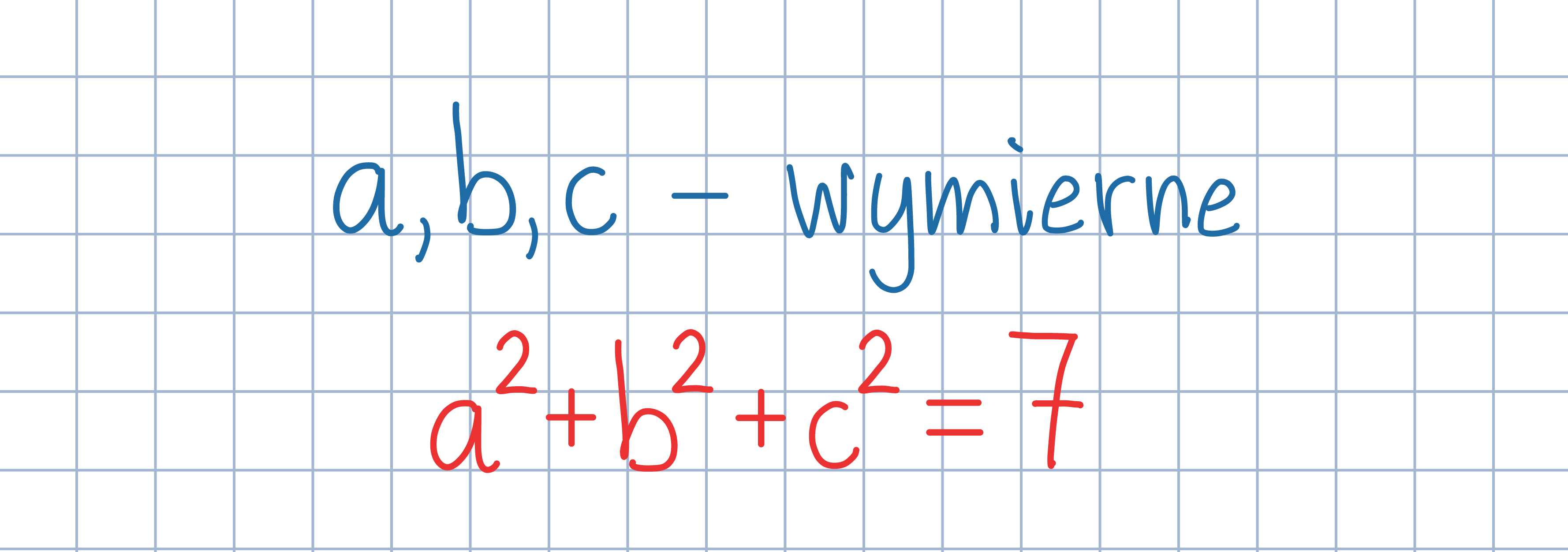 Odp.: Taki rozkład nie jest możliwy.
Odp.: Taki rozkład nie jest możliwy.Jeśli a/d, b/d, c/d są liczbami wymiernymi spełniającymi dany warunek, gdzie a, b, c, d są liczbami całkowitymi, to dana w treści zadania zależność przybiera postać a^2+b^2+c^2=7d^2. Rozpatrz dwa przypadki: d – parzyste, d – nieparzyste.

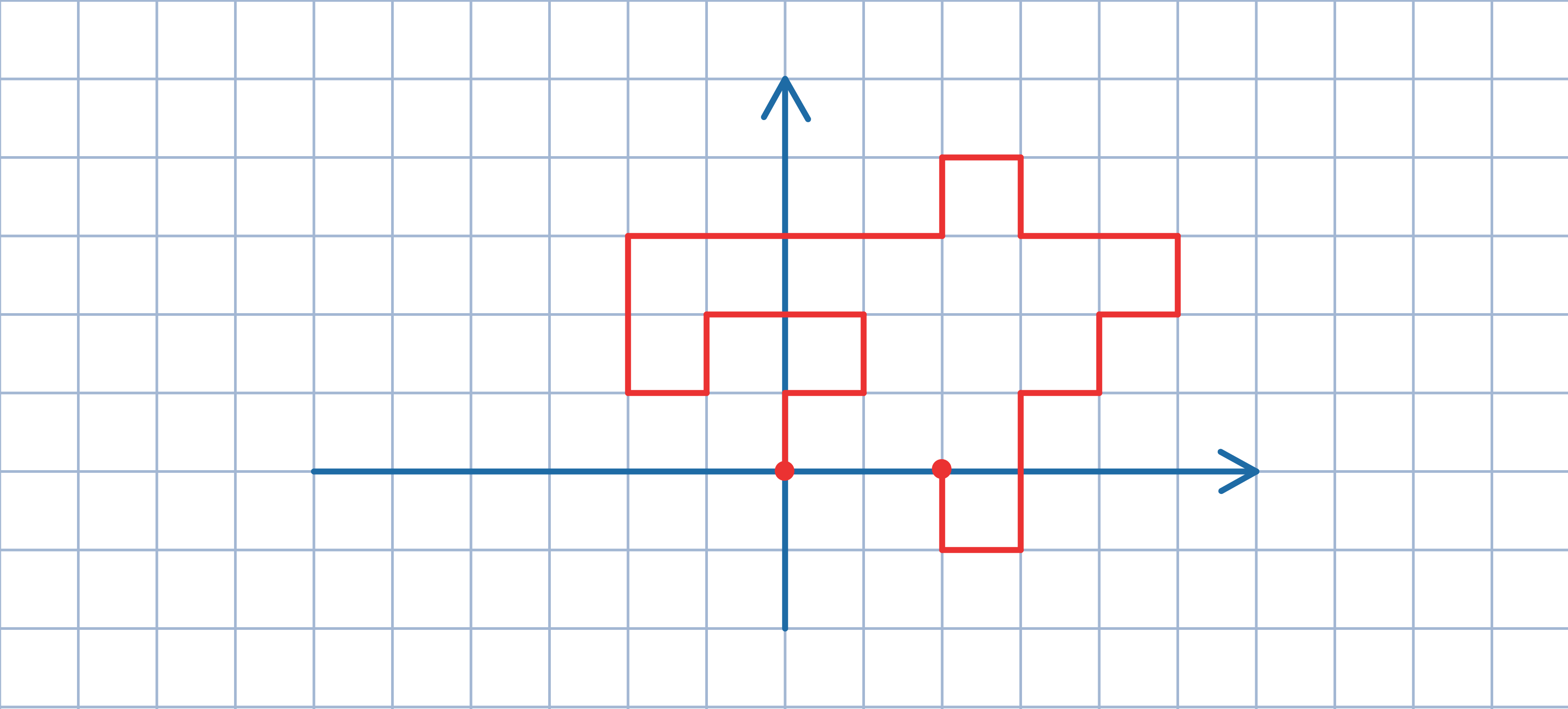 Odp.: 2n po n, tzn. (2n)!/(n!∙n!).
Odp.: 2n po n, tzn. (2n)!/(n!∙n!).Każdą drogę o długości n startującą z punktu (0,0) zakoduj przy pomocy 2n cyfr, z których każda jest równa 0 lub 1, w następujący sposób: 01 – ruch w lewo, 10 – ruch w prawo, 11 – ruch w górę, 00 – ruch w dół.
 Uzasadnij, że jeśli p jest liczbą pierwszą, a liczba całkowita r nie jest podzielna
przez p, to dla dowolnej liczby całkowitej a liczby a,
Uzasadnij, że jeśli p jest liczbą pierwszą, a liczba całkowita r nie jest podzielna
przez p, to dla dowolnej liczby całkowitej a liczby a,
 Odp.: 1000=3+3+...+3+4 (332 trójki).
Odp.: 1000=3+3+...+3+4 (332 trójki).Uzasadnij, że jeśli n>4 jest jednym ze składników, to większy iloczyn uzyskamy, jeśli zastąpimy go przez sumę 2+(n-2). Zauważ także, że 3∙3>2∙2∙2.
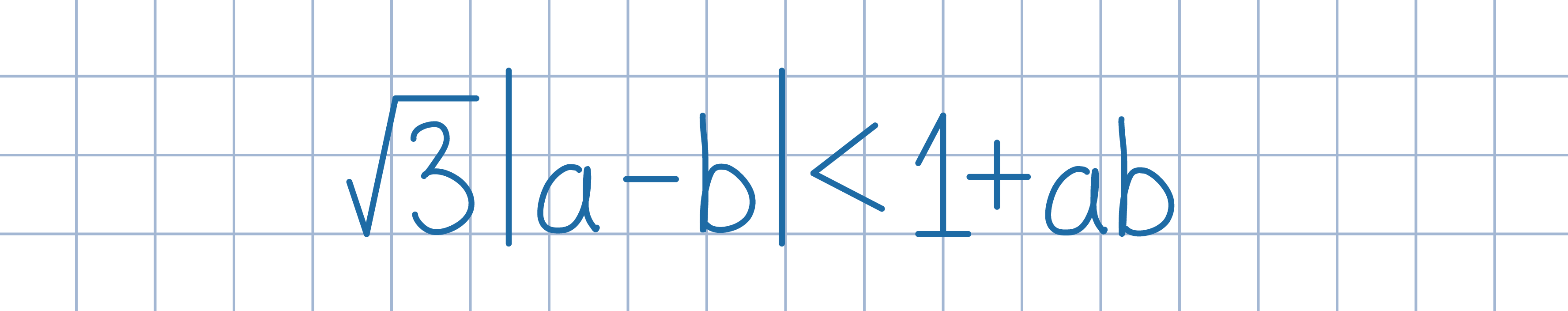 Dla każdej liczby a spośród danych siedmiu wyznacz liczbę x z przedziału
(-π,π), dla której
Dla każdej liczby a spośród danych siedmiu wyznacz liczbę x z przedziału
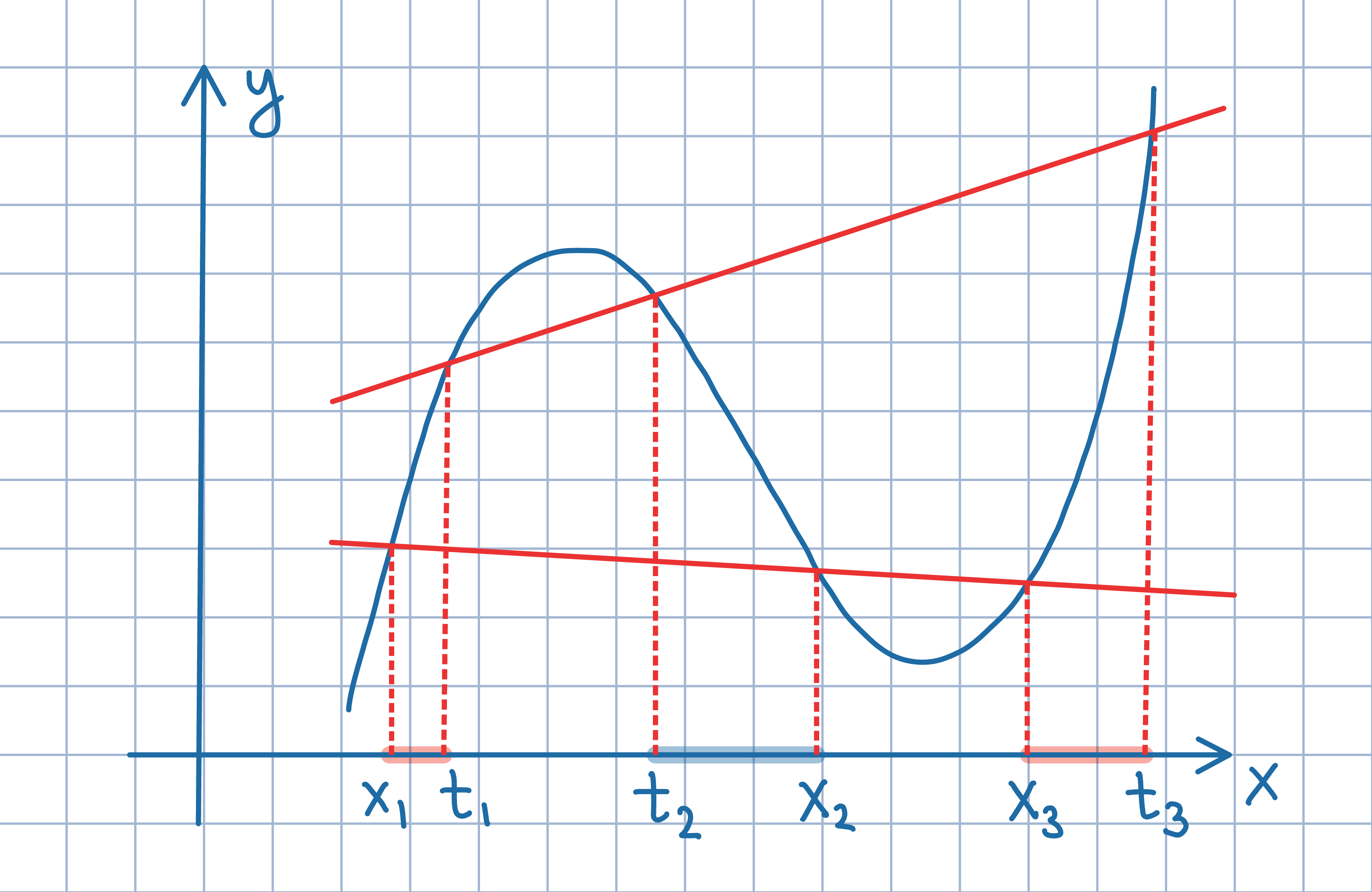
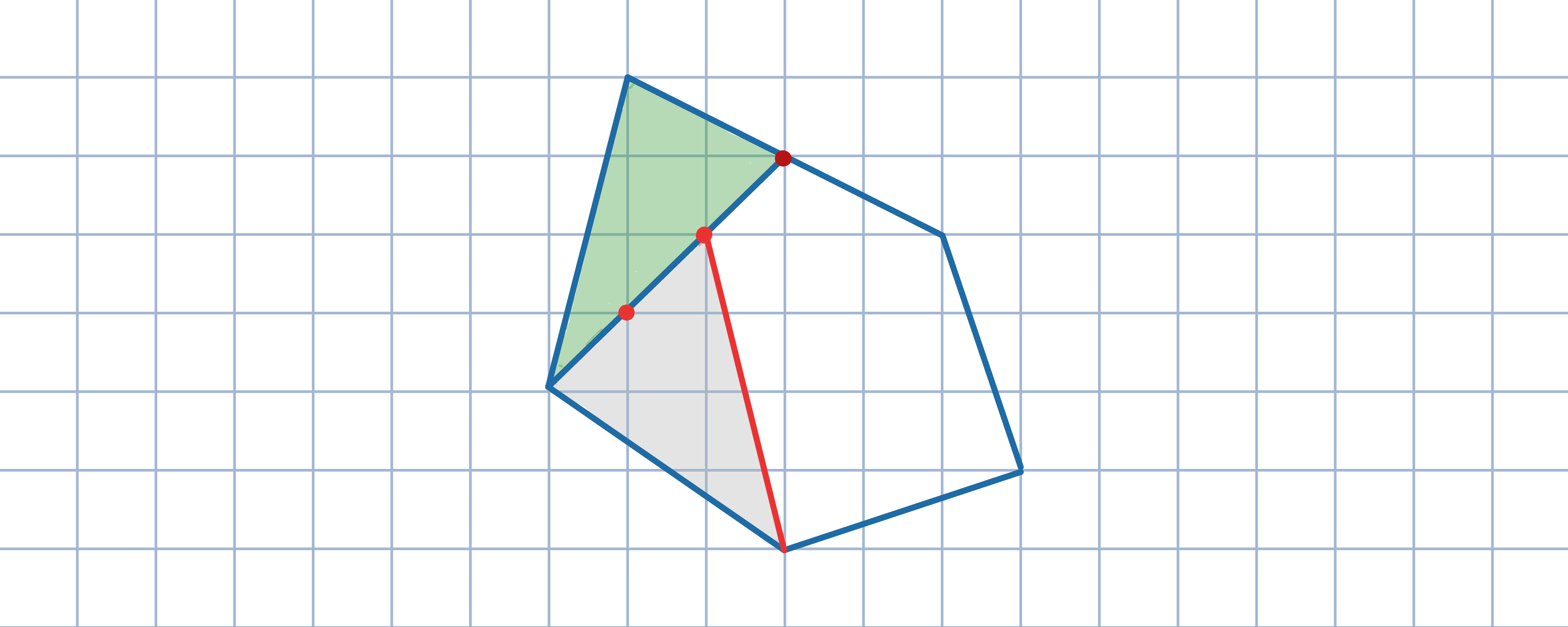
(-π,π), dla której 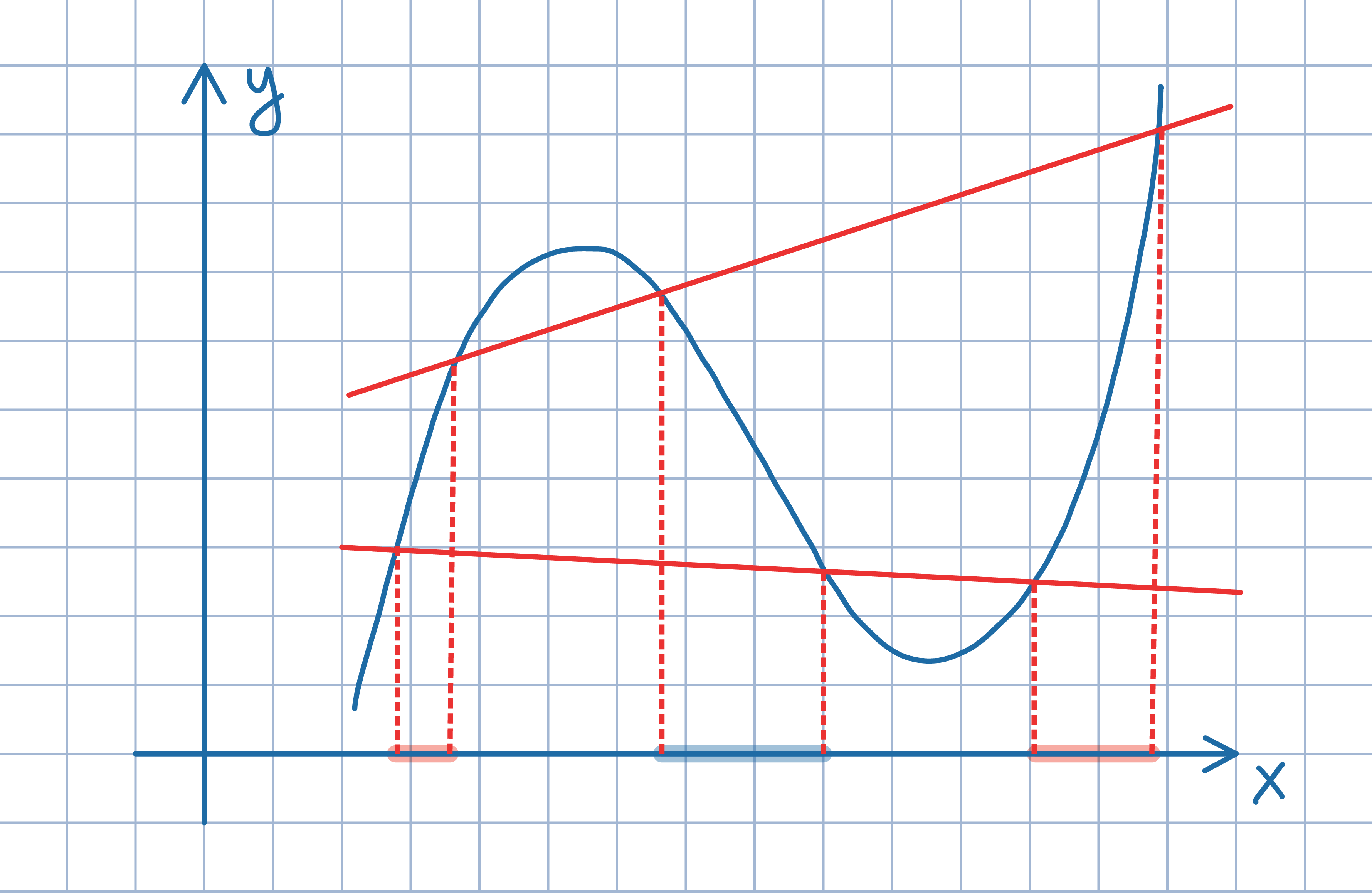 Oznacz końce uzyskanych odcinków jak na poniższym rysunku. Następnie, wykorzystując
wzory Viete'a dla wielomianów trzeciego stopnia, uzasadnij, że
x_1+x_2+x_3=t_1+t_2+t_3.
Oznacz końce uzyskanych odcinków jak na poniższym rysunku. Następnie, wykorzystując
wzory Viete'a dla wielomianów trzeciego stopnia, uzasadnij, że
x_1+x_2+x_3=t_1+t_2+t_3.
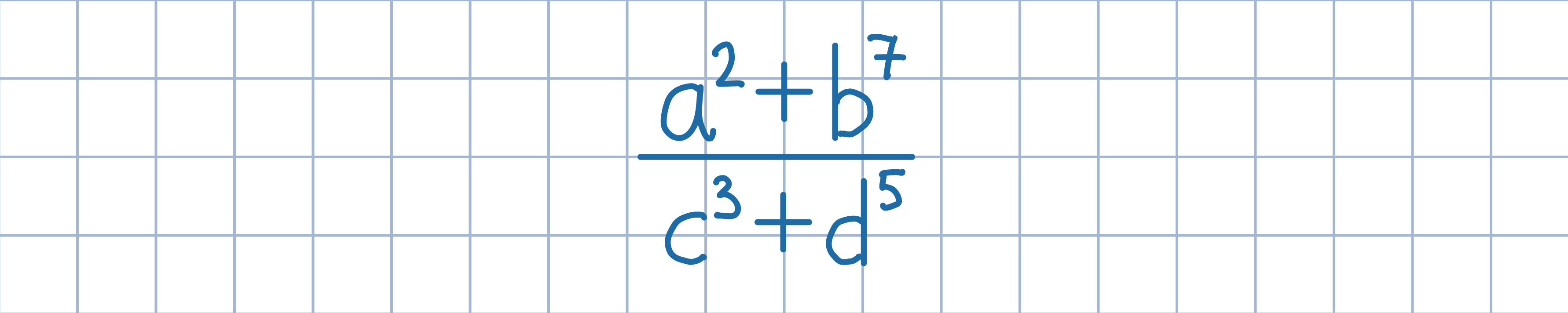
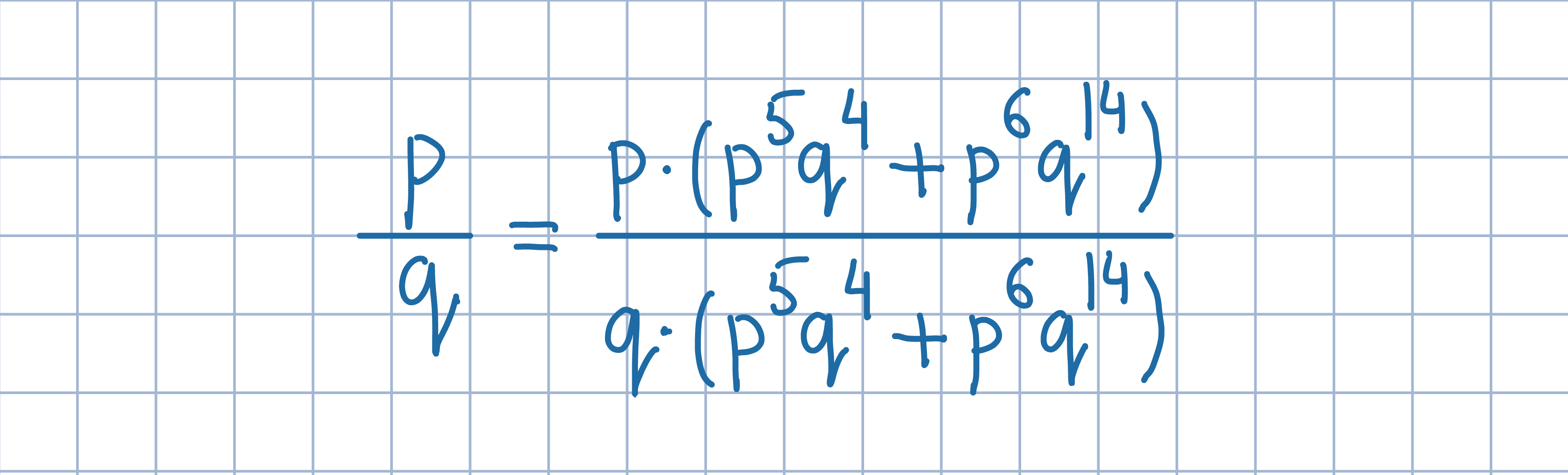
 Wykorzystaj poniższe nierówności.
Wykorzystaj poniższe nierówności.

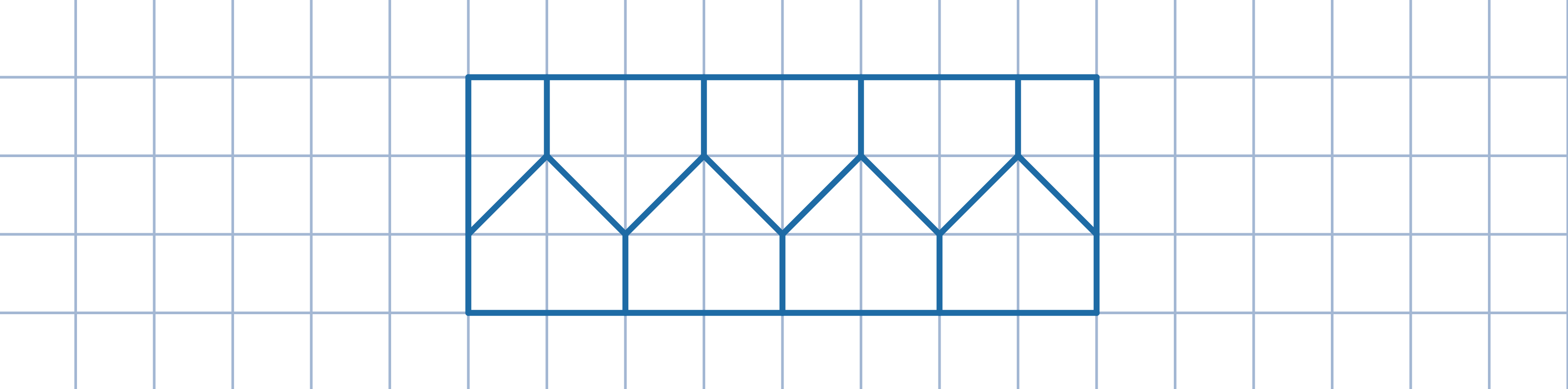
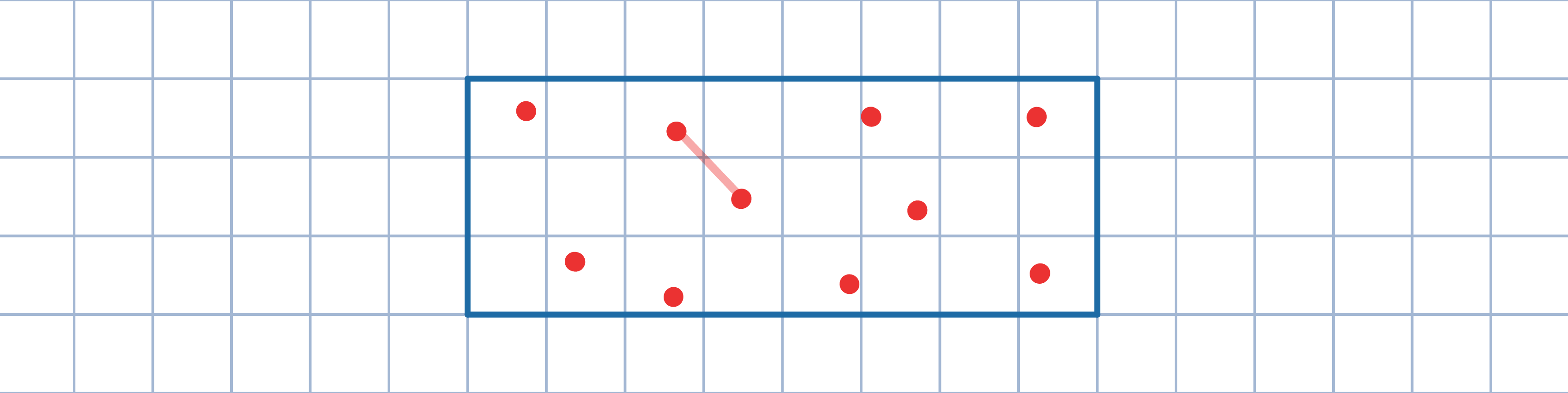 Podziel dany prostokąt na 9 wielokątów w sposób przedstawiony na rysunku.
Zauważ, że pewne dwa spośród danych punktów leżą w tym samym wielokącie.
Podziel dany prostokąt na 9 wielokątów w sposób przedstawiony na rysunku.
Zauważ, że pewne dwa spośród danych punktów leżą w tym samym wielokącie.
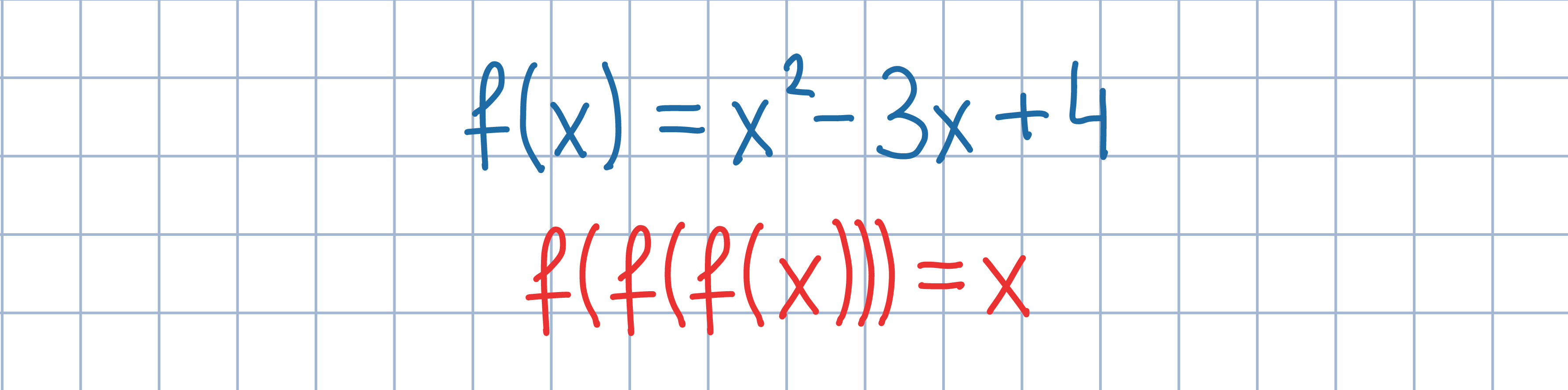 Odp.: x=2.
Odp.: x=2.Uzasadnij, że dla dowolnej liczby rzeczywistej x spełniona jest poniższa nierówność, przy czym równość ma miejsce wtedy i tylko wtedy, gdy x=2.
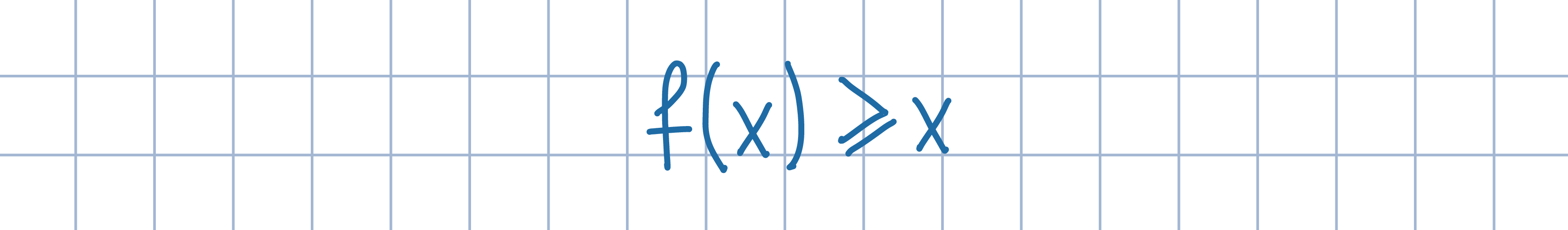
 Jeśli na obwodzie pięciokąta jest jeszcze co najmniej jeden punkt kratowy
poza wierzchołkami, to skonstruuj najpierw pięciokąt, na którego obwodzie jedynymi punktami kratowymi będą
jego wierzchołki. Następnie uzasadnij, że środek odcinka łączącego pewne dwa wierzchołki jest
punktem kratowym.
Jeśli na obwodzie pięciokąta jest jeszcze co najmniej jeden punkt kratowy
poza wierzchołkami, to skonstruuj najpierw pięciokąt, na którego obwodzie jedynymi punktami kratowymi będą
jego wierzchołki. Następnie uzasadnij, że środek odcinka łączącego pewne dwa wierzchołki jest
punktem kratowym.
 Odp.: 2^(n-1).
Odp.: 2^(n-1).Zauważ, że na końcu kolejki może stać albo osoba najwyższa albo najniższa.
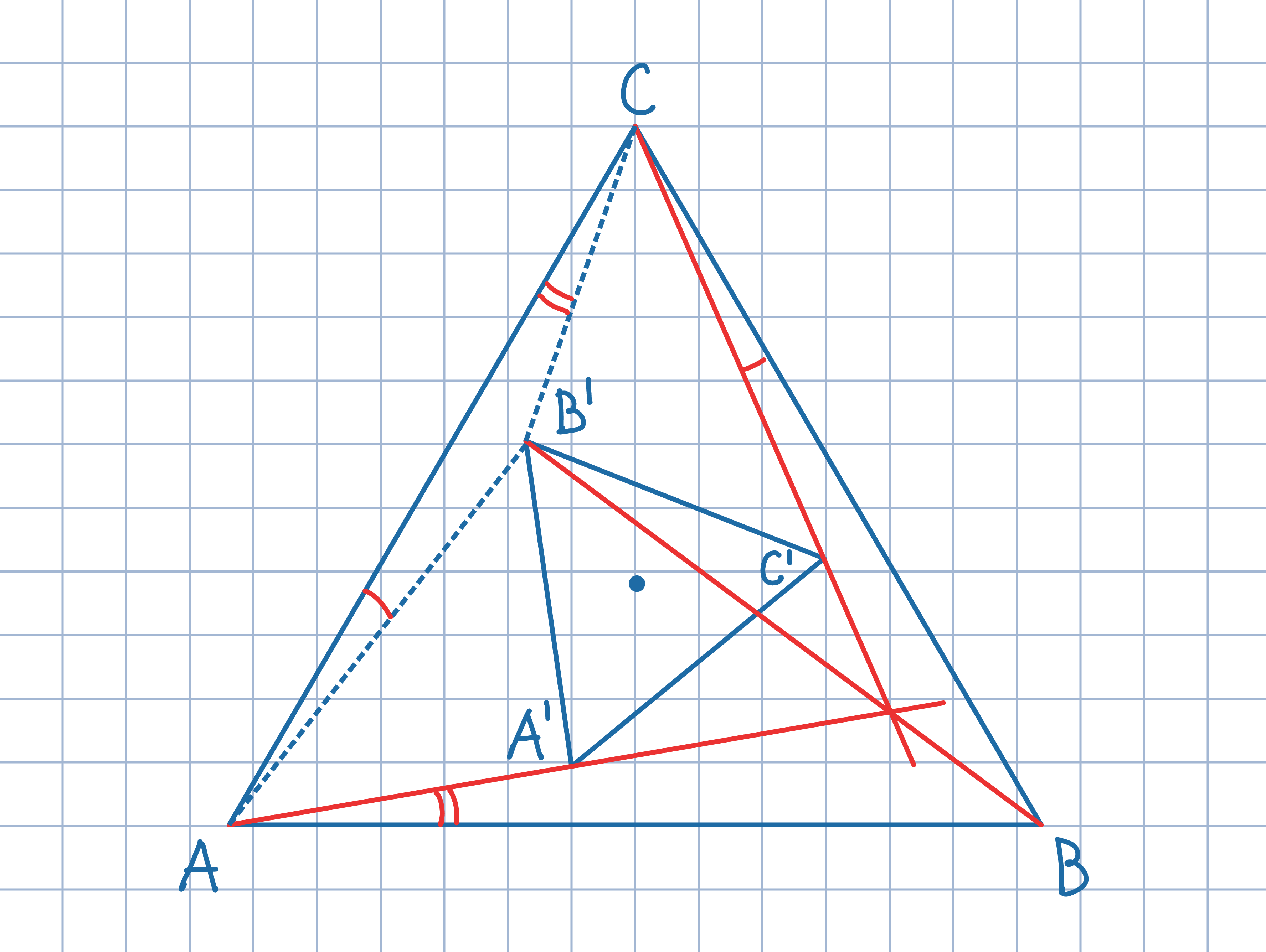
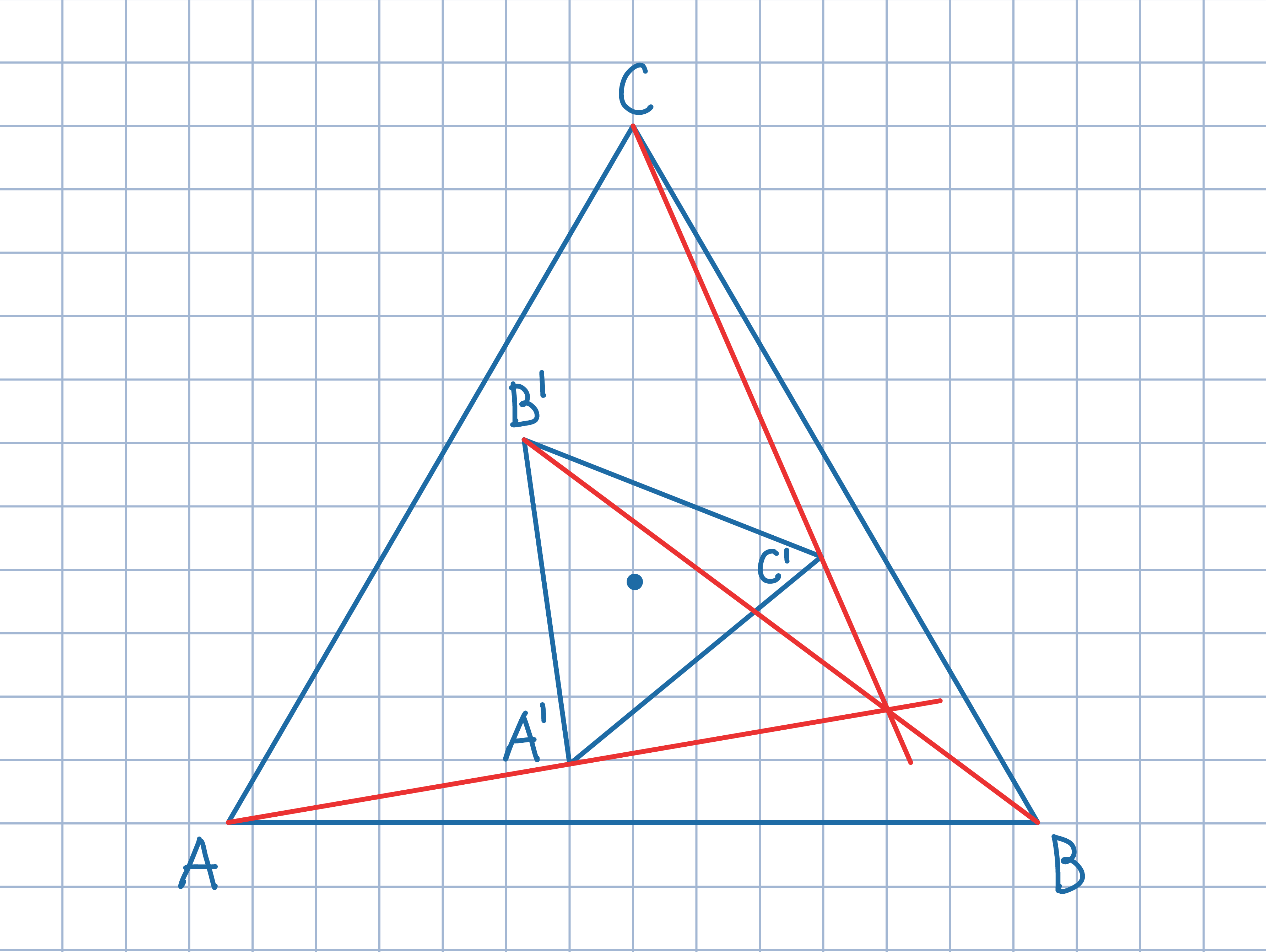 Rozpatrując pewien obrót, uzasadnij, że
kąty B'AC i C'CB są równe, a także, że kąty B'CA i A'AB są równe. Wykorzystaj
trygonometryczną wersję twierdzenia Cevy.
Rozpatrując pewien obrót, uzasadnij, że
kąty B'AC i C'CB są równe, a także, że kąty B'CA i A'AB są równe. Wykorzystaj
trygonometryczną wersję twierdzenia Cevy.
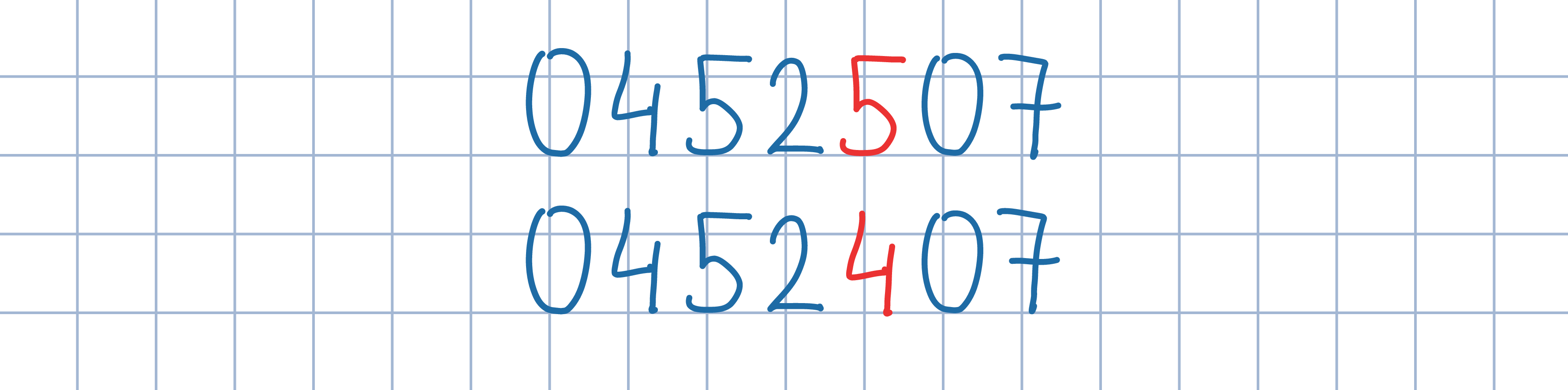 Odp.: 10^(n–1).
Odp.: 10^(n–1).Uzasadnij, że jeśli w banku byłoby więcej niż
Aby skonstruować przykład
 Uzasadnij, że jeśli różne liczby a, b są całkowite, to liczba
w(a)–w(b) jest podzielna przez a–b.
Uzasadnij, że jeśli różne liczby a, b są całkowite, to liczba
w(a)–w(b) jest podzielna przez a–b.
 Przypuśćmy, że obie funkcje kwadratowe f(x) i g(x) nie mają rzeczywistych
pierwiastków. Rozpatrz wtedy funkcję f(x)+g(x).
Przypuśćmy, że obie funkcje kwadratowe f(x) i g(x) nie mają rzeczywistych
pierwiastków. Rozpatrz wtedy funkcję f(x)+g(x).

 Warunek p_n=5 oznacza, że iloczyn p_1p_2...p_(n-1) jest
liczbą postaci 2^a3^b5^c–1 dla pewnych liczb całkowitych nieujemnych a, b, c. Uzasadnij, że a=0, b=0 i doprowadź do sprzeczności.
Warunek p_n=5 oznacza, że iloczyn p_1p_2...p_(n-1) jest
liczbą postaci 2^a3^b5^c–1 dla pewnych liczb całkowitych nieujemnych a, b, c. Uzasadnij, że a=0, b=0 i doprowadź do sprzeczności.
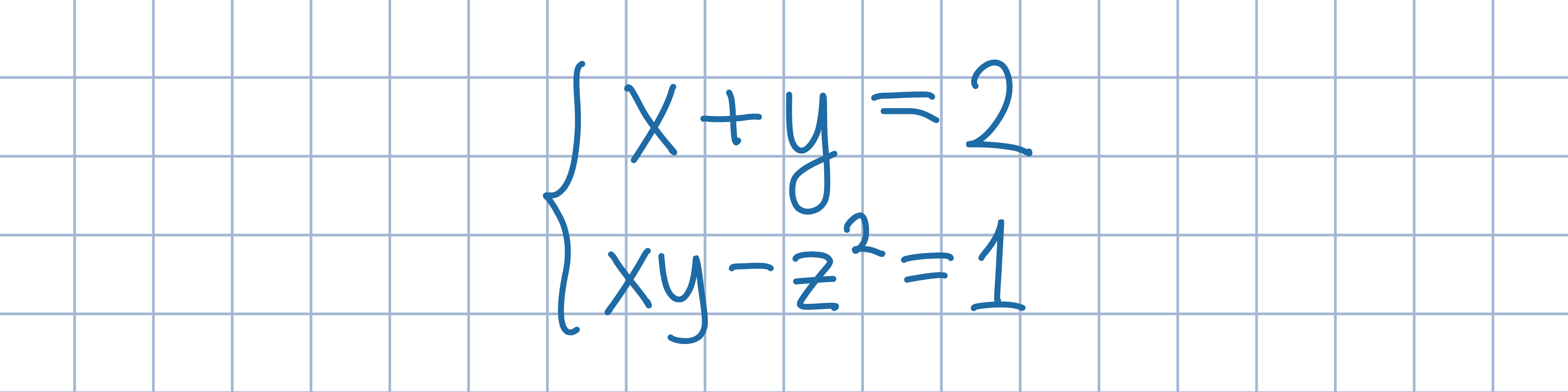 Odp.: x=y=1, z=0.
Odp.: x=y=1, z=0.Uzasadnij najpierw, że obie liczby x, y są nieujemne. Następnie wykorzystaj nierówność między średnią arytmetyczną a geometryczną dla liczb x, y.
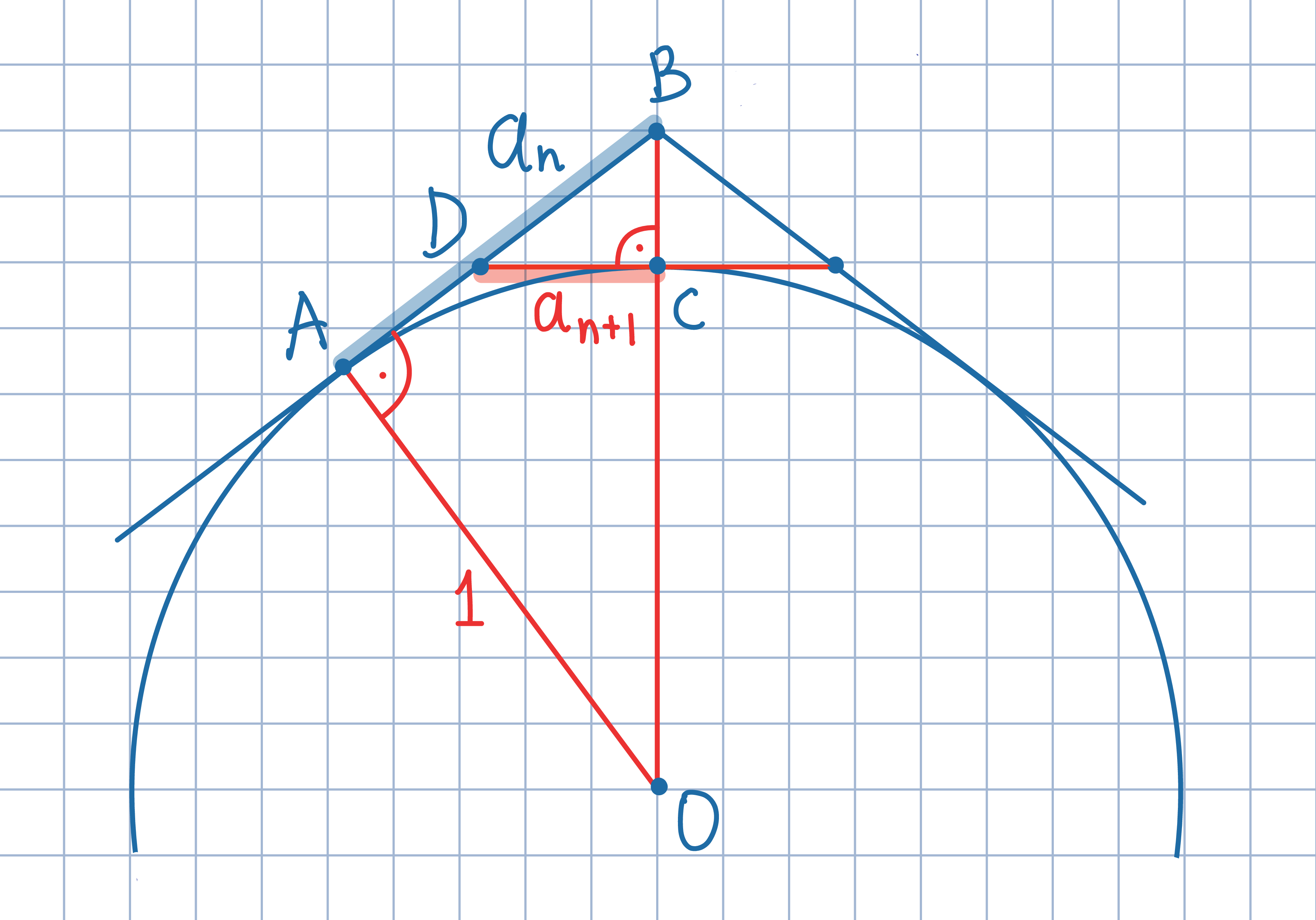
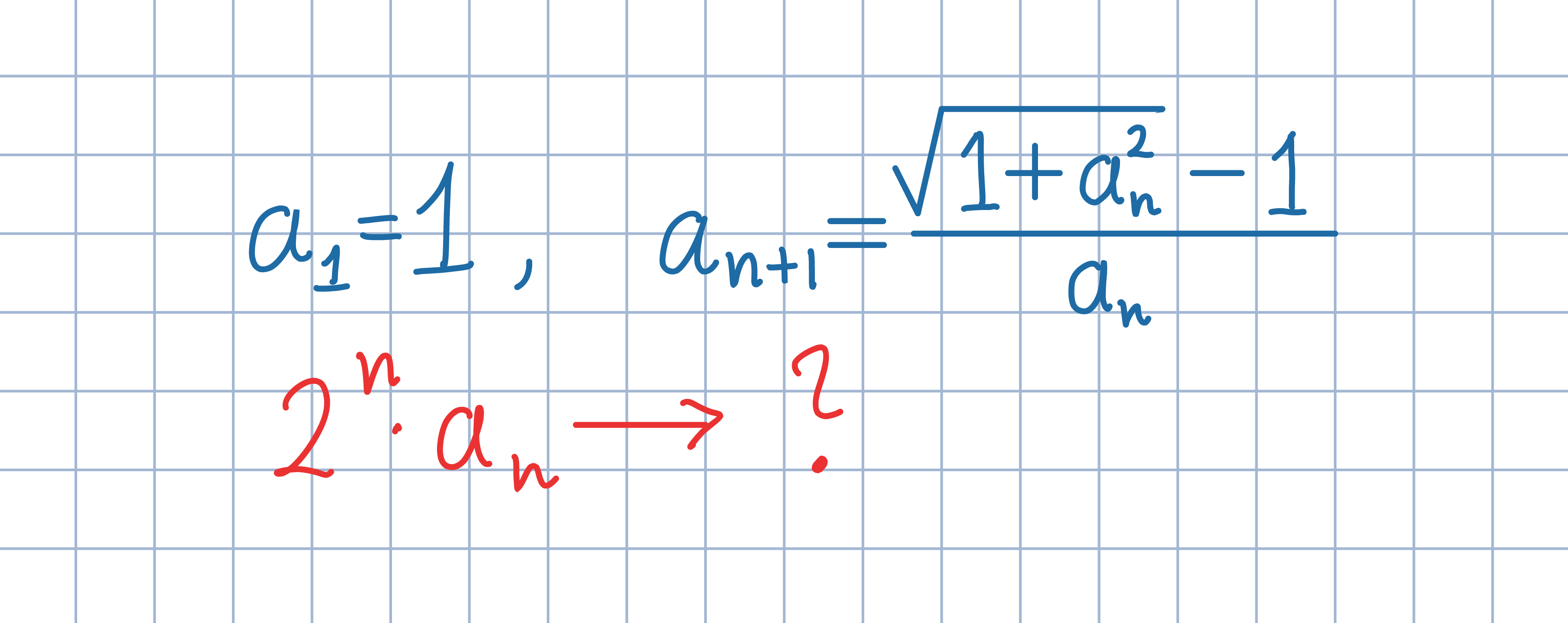 Odp.: a=pi/2.
Odp.: a=pi/2.Wykorzystując podobieństwo trójkątów ABO oraz CBD, uzasadnij, że 2a_n jest długością boku 2^(n+1)-kąta foremnego opisanego na okręgu o promieniu 1.
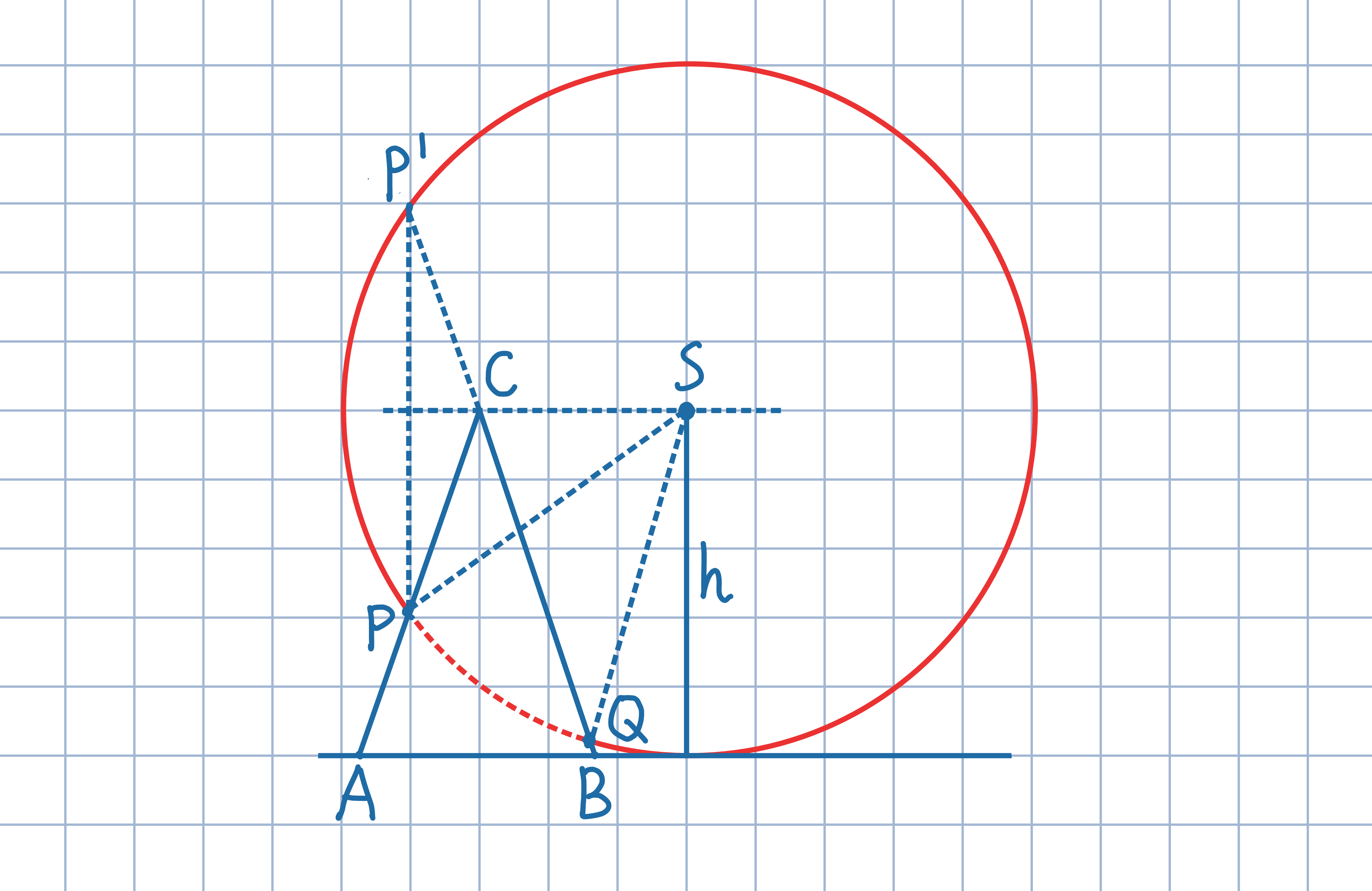
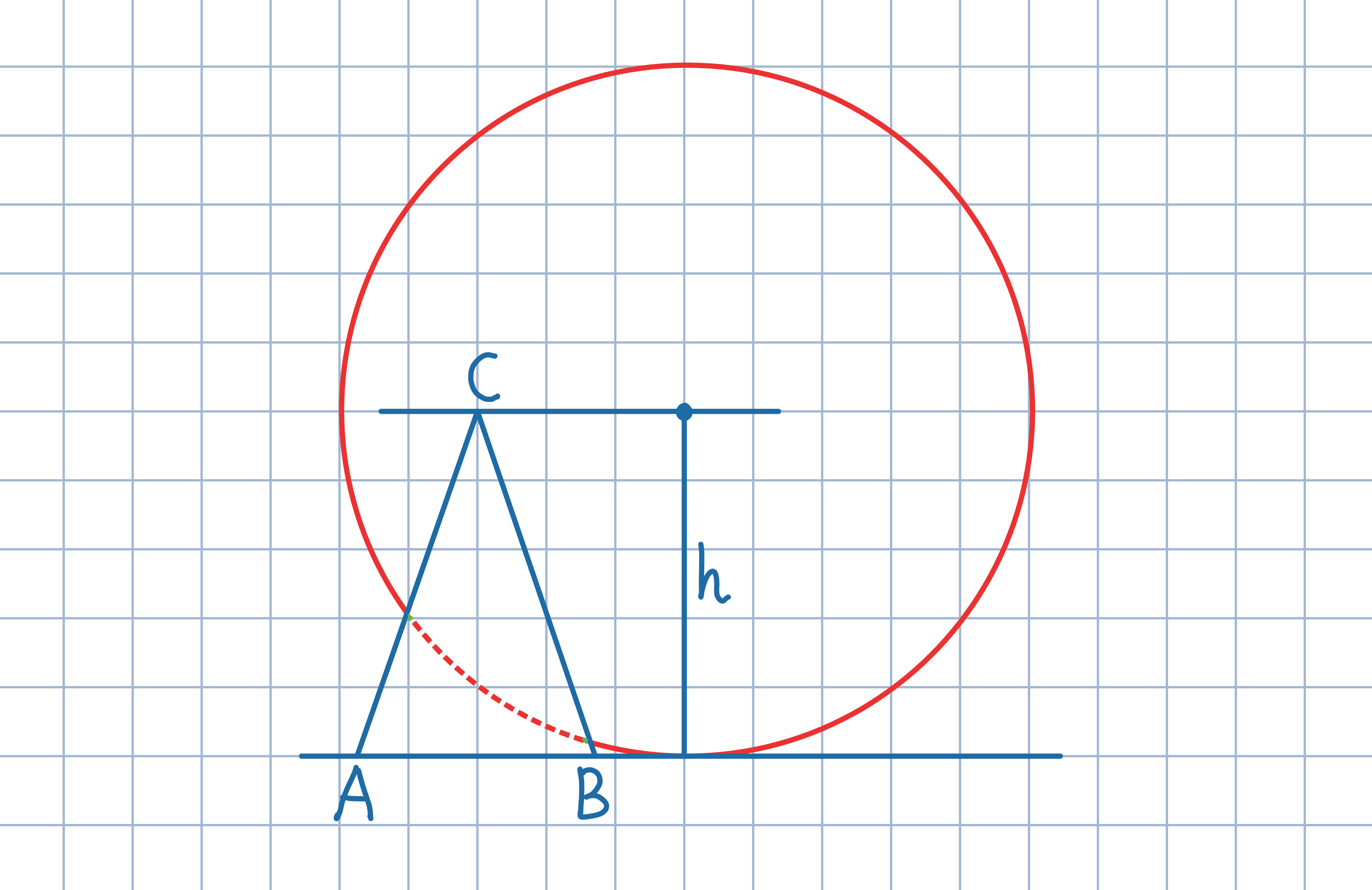 Odp.: Długość łuku PQ jest stała, niezależnie od położenia okręgu.
Odp.: Długość łuku PQ jest stała, niezależnie od położenia okręgu.Oznacz przez P, Q końce rozpatrywanego łuku, przez S – środek okręgu. Niech P' będzie obrazem symetrycznym punktu P względem prostej CS. Uzasadnij, że punkt P' leży zarówno na okręgu, jak i na prostej BC. Wywnioskuj stąd, że kąty ACB i PSQ są równe.
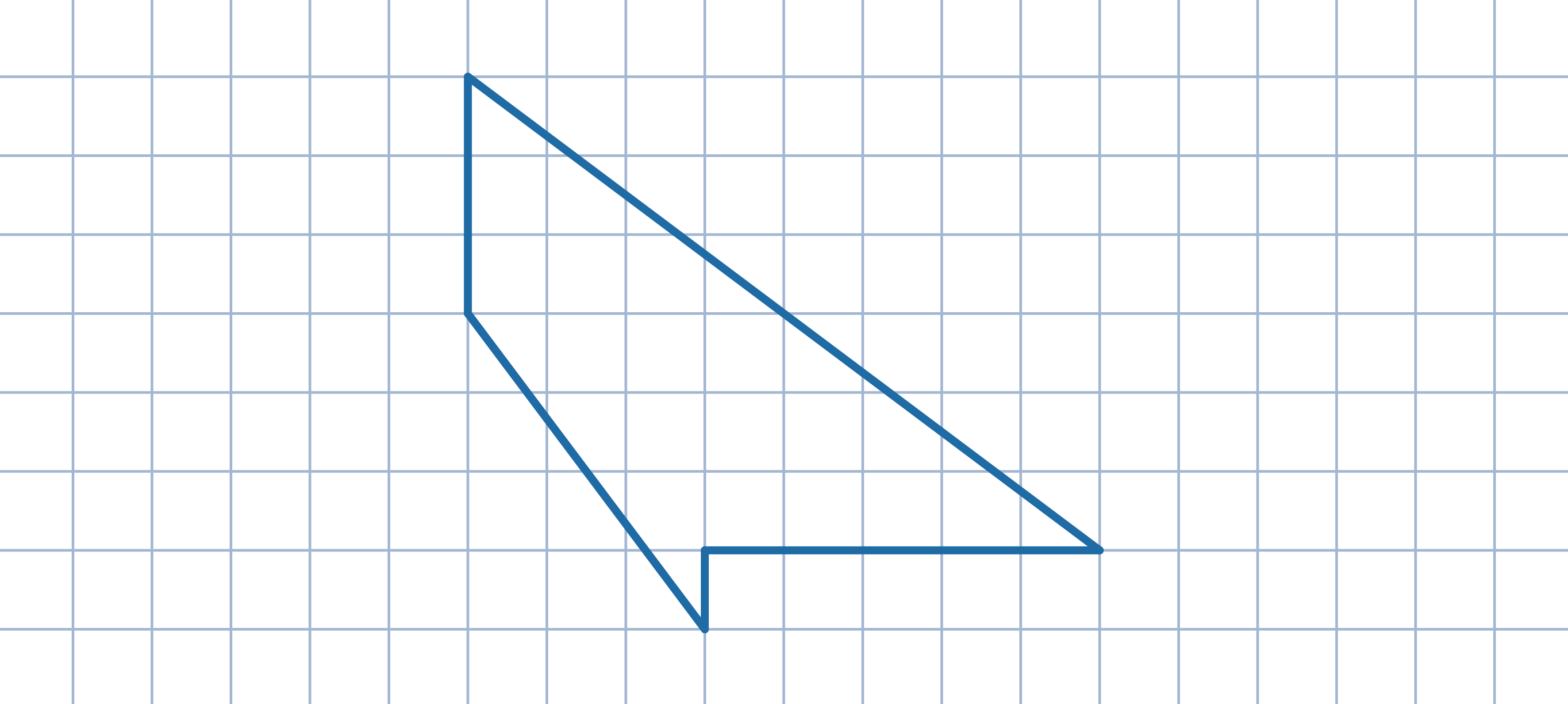
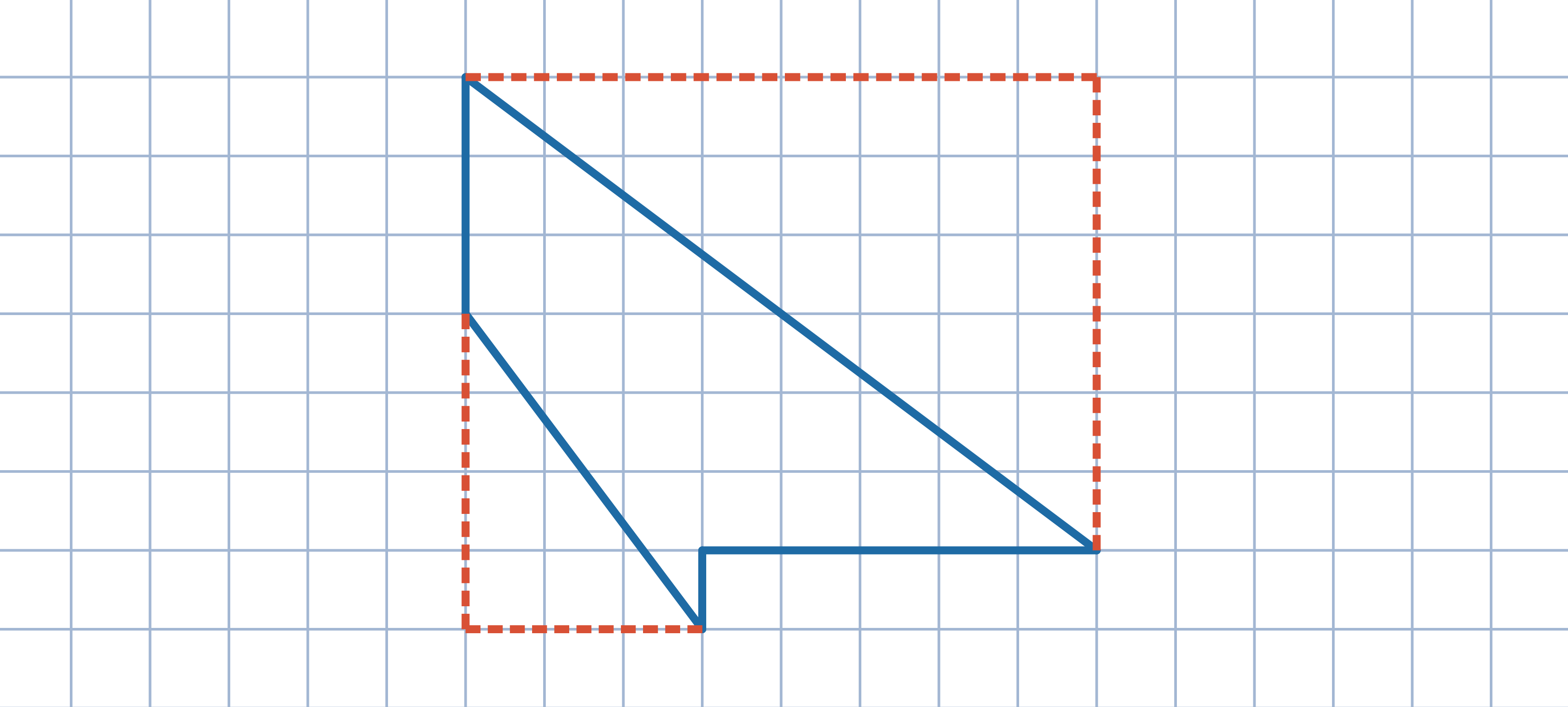
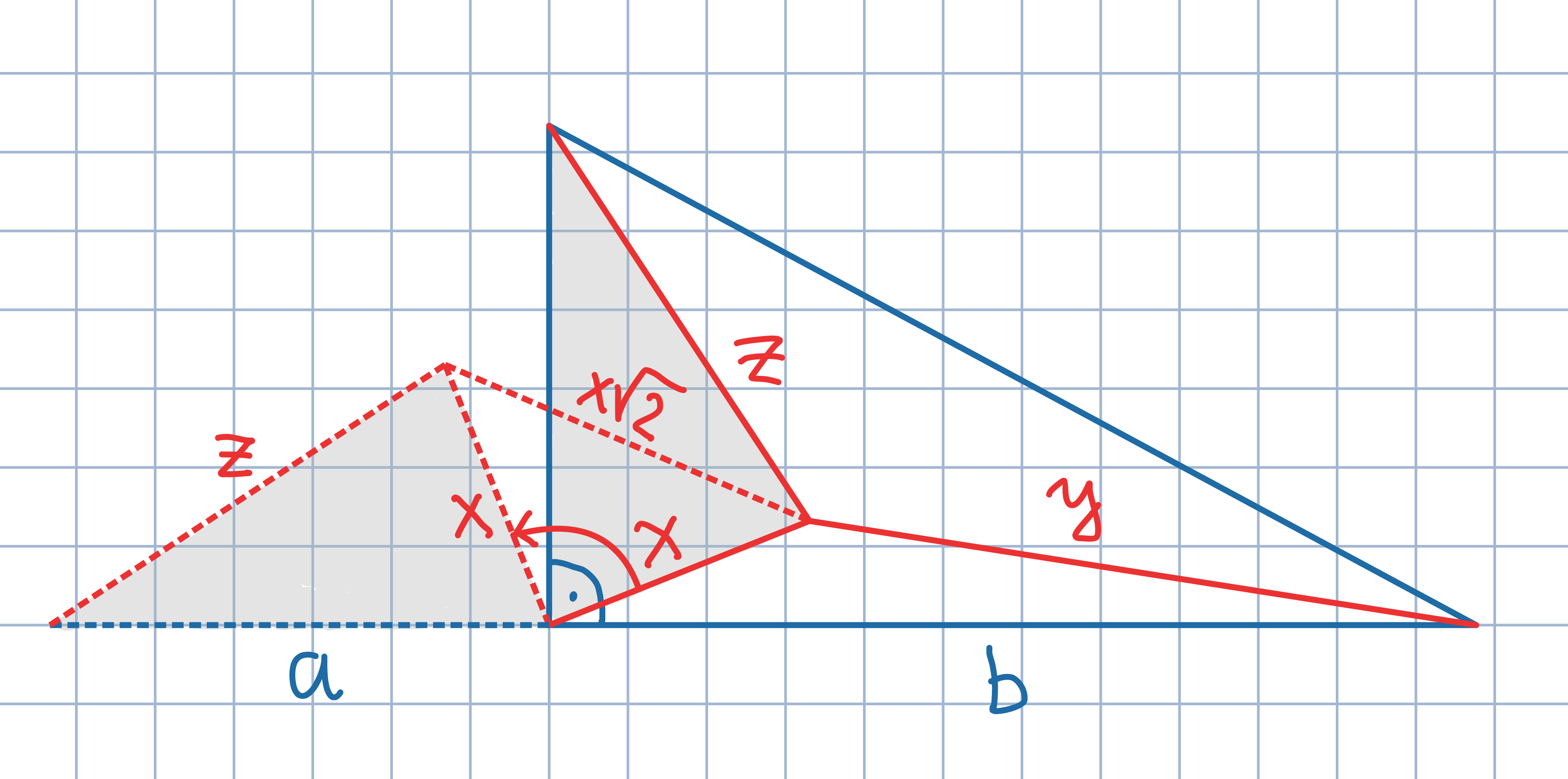
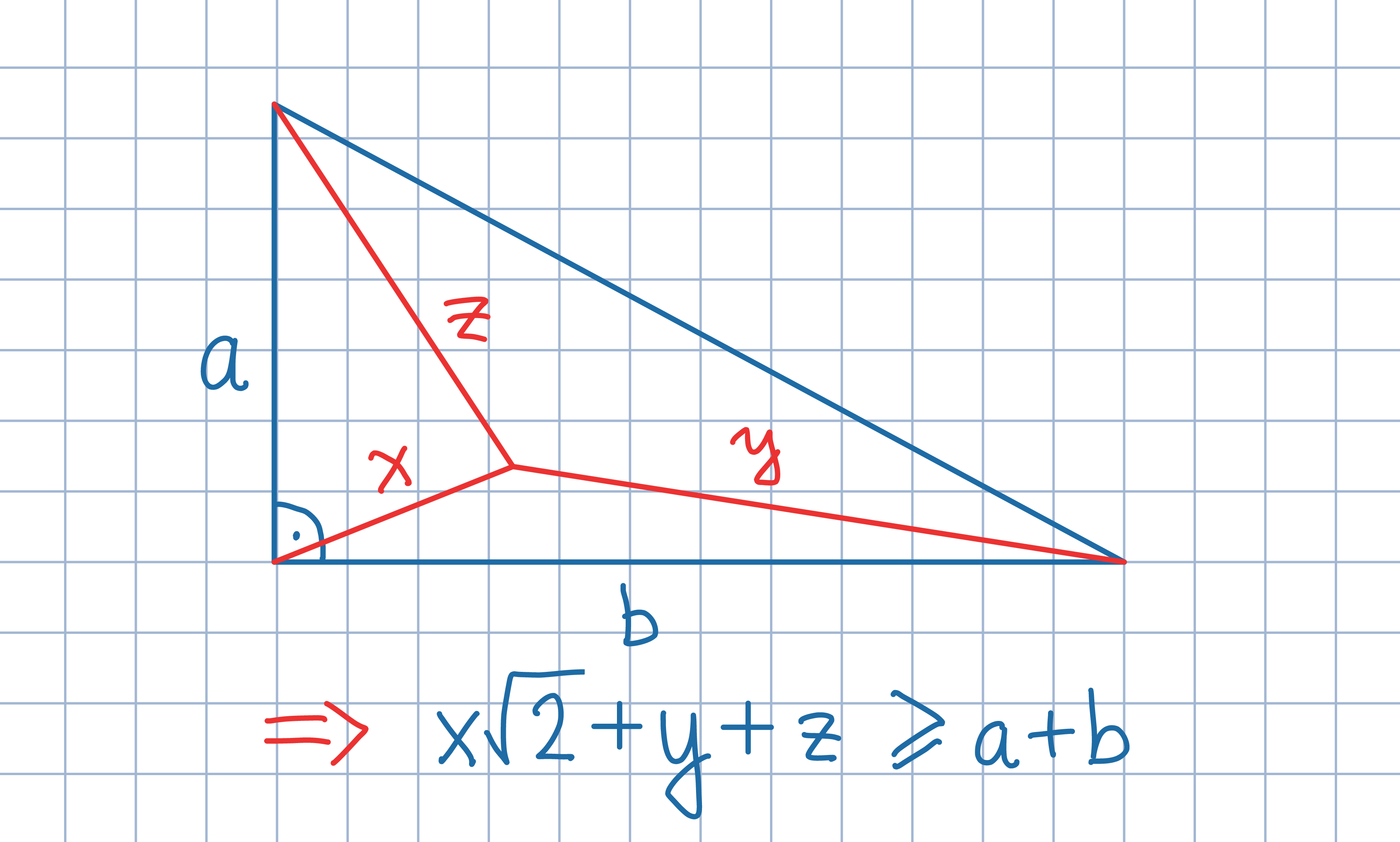 Obróć szary trójkąt leżący wewnątrz danego trójkąta prostokątnego
o 90 stopni
wokół wierzchołka kąta prostego.
Obróć szary trójkąt leżący wewnątrz danego trójkąta prostokątnego
o 90 stopni
wokół wierzchołka kąta prostego.
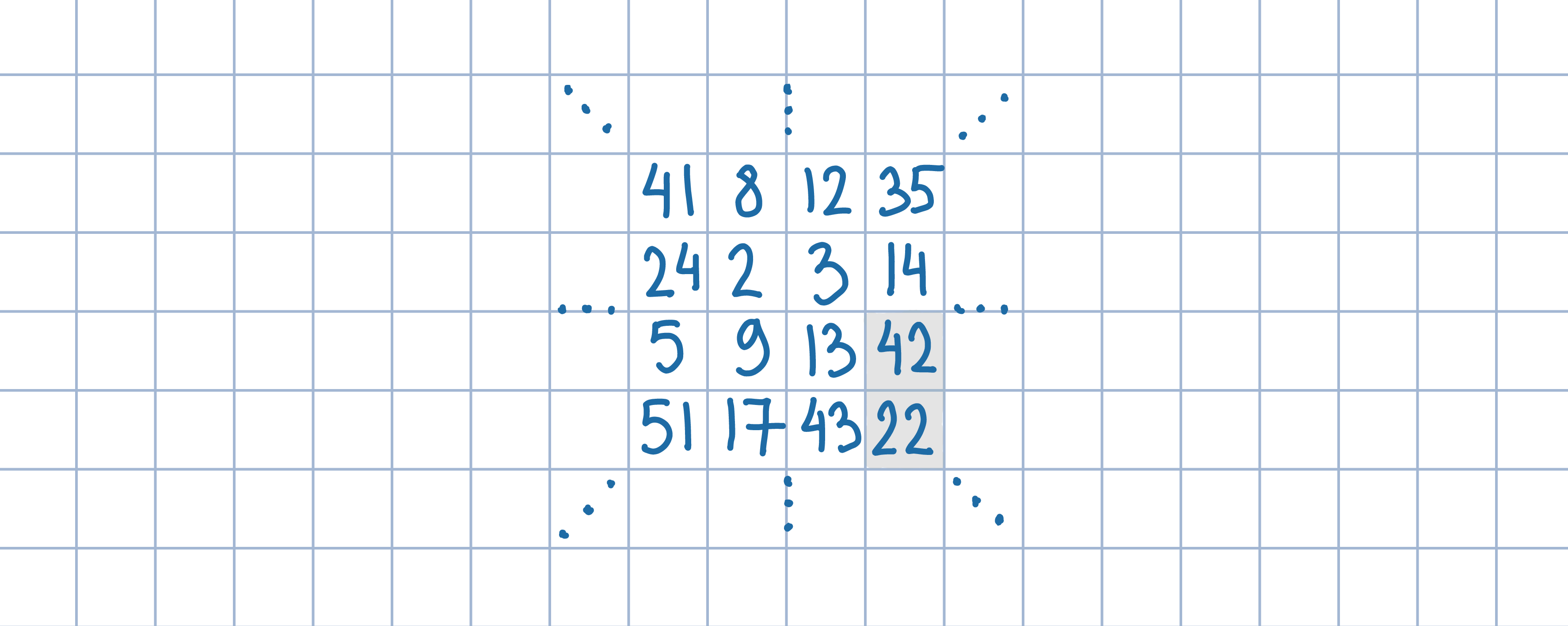 Przypuśćmy, wbrew tezie, że liczby wpisane w każde dwa sąsiednie
pola różnią się o co najwyżej a. Rozpatrz kwadrat o boku n składający się z n^2 pól.
Uzasadnij, że różnica największej i najmniejszej liczby z tego kwadratu jest nie mniejsza od
n^2–1. Następnie uzasadnij, że te dwie liczby różnią się
o co najwyżej 2(n-1)a. Dobierając odpowiednio dużą liczbę n, doprowadź do sprzeczności.
Przypuśćmy, wbrew tezie, że liczby wpisane w każde dwa sąsiednie
pola różnią się o co najwyżej a. Rozpatrz kwadrat o boku n składający się z n^2 pól.
Uzasadnij, że różnica największej i najmniejszej liczby z tego kwadratu jest nie mniejsza od
n^2–1. Następnie uzasadnij, że te dwie liczby różnią się
o co najwyżej 2(n-1)a. Dobierając odpowiednio dużą liczbę n, doprowadź do sprzeczności.
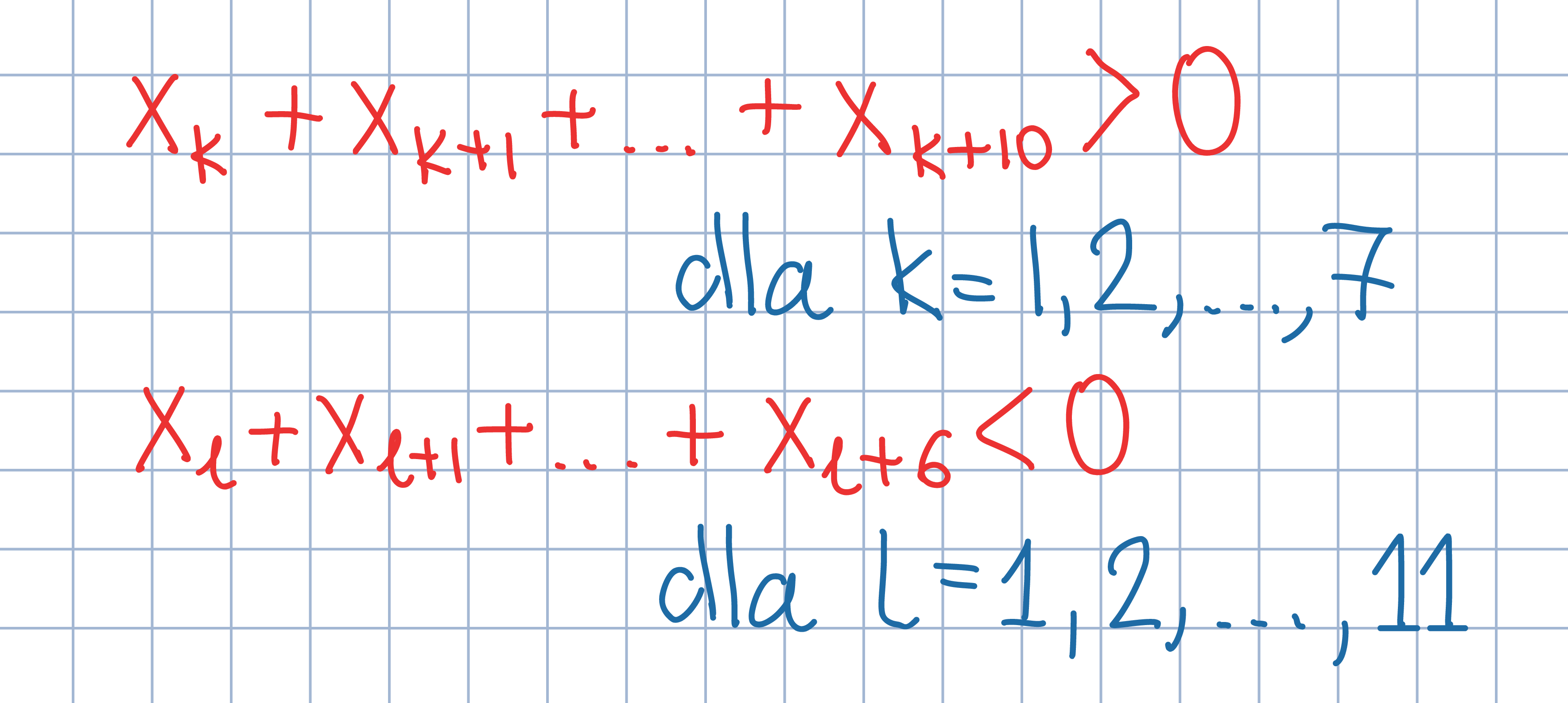 Odp.: Taki ciąg liczb nie istnieje.
Odp.: Taki ciąg liczb nie istnieje.Zapisz wyrazy x_i danego ciągu w tabeli w poniższy sposób. Jaki znak ma suma wszystkich liczb w tej tabeli?
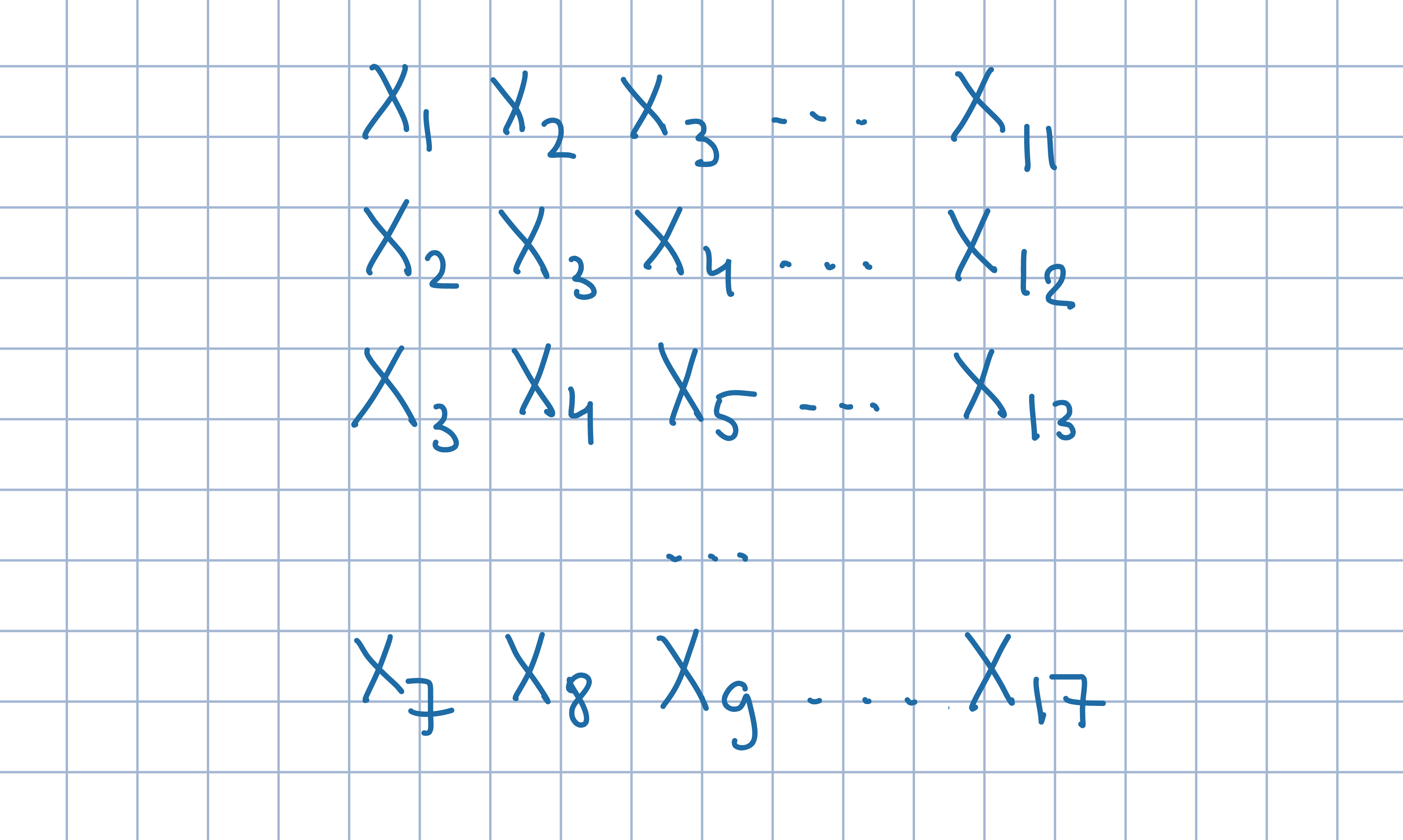
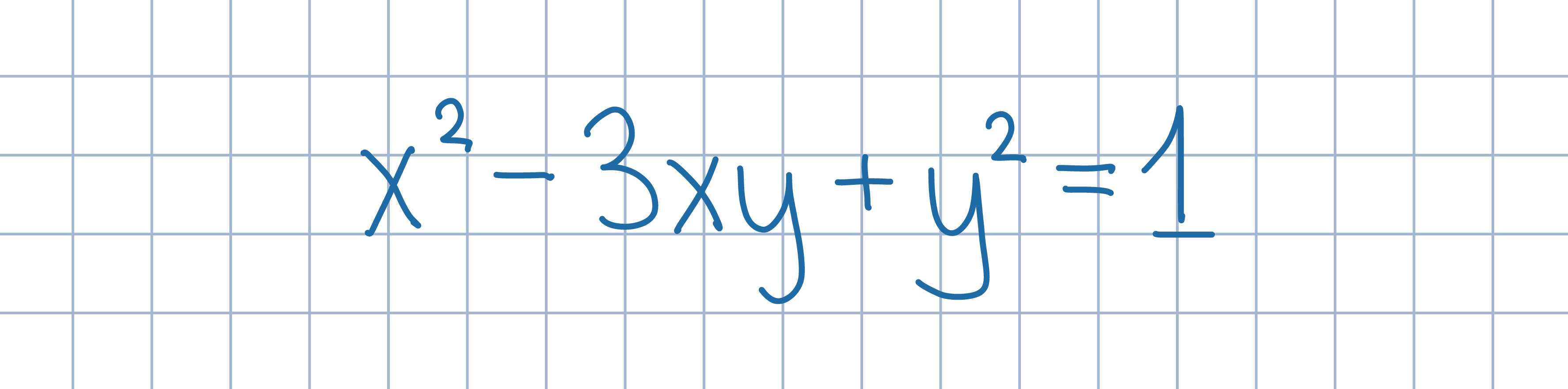 Zauważ, że x=0, y=1 jest rozwiązaniem danego równania. Uzasadnij następnie, że jeśli para (x,y) spełnia dane równanie, to także para (y,3y–x) spełnia to równanie.
Zauważ, że x=0, y=1 jest rozwiązaniem danego równania. Uzasadnij następnie, że jeśli para (x,y) spełnia dane równanie, to także para (y,3y–x) spełnia to równanie.
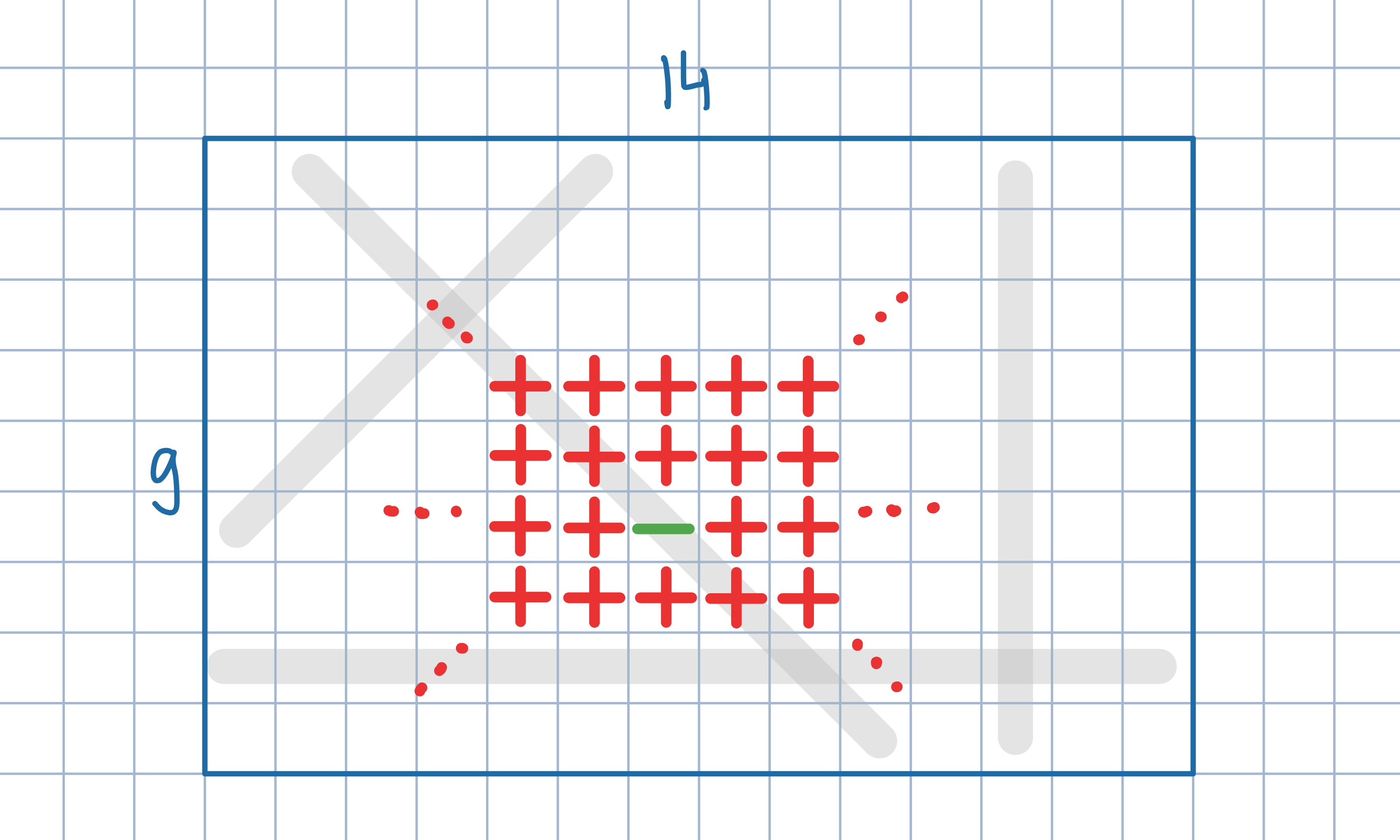 Odp.: Uzyskanie tablicy z samych plusów jest możliwe jedynie wtedy, gdy znak „–”
znajduje się w jednym z rogów prostokąta.
Odp.: Uzyskanie tablicy z samych plusów jest możliwe jedynie wtedy, gdy znak „–”
znajduje się w jednym z rogów prostokąta.W przypadku, gdy znak „–” nie znajduje się w rogu prostokąta, wyróżnij 8 pól w sposób pokazany na poniższym rysunku. Zauważ, że podczas wykonywania ruchu nie zmienia się parzystość liczby plusów na wyróżnionych polach.
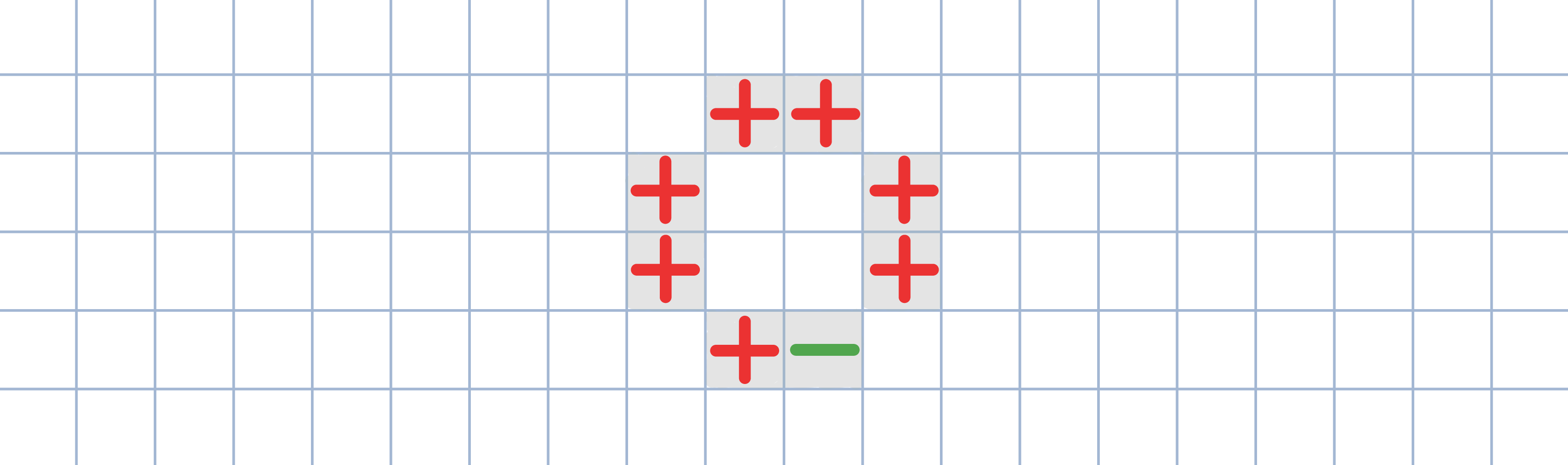
 Indukcja. Dla n=1 teza jest oczywiście spełniona.
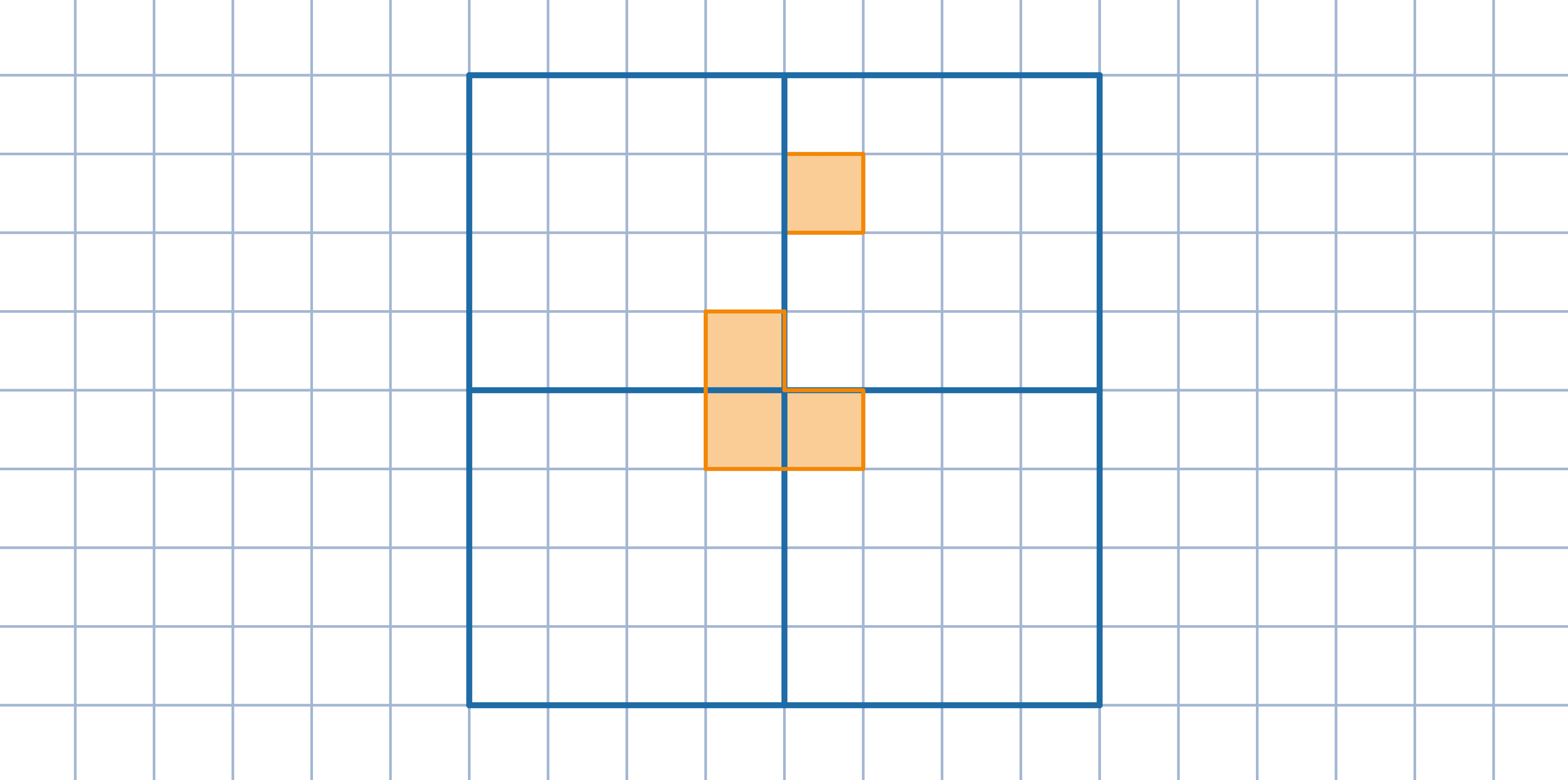
Krok indukcyjny. Podziel kwadrat o boku 2^(n+1) na cztery przystające kwadraty, każdy o boku 2^n. Następnie umieść jeden klocek w centralnej części dużego kwadratu w sposób przedstawiony na rysunku. Skorzystaj z założenia indukcyjnego.
Indukcja. Dla n=1 teza jest oczywiście spełniona.
Krok indukcyjny. Podziel kwadrat o boku 2^(n+1) na cztery przystające kwadraty, każdy o boku 2^n. Następnie umieść jeden klocek w centralnej części dużego kwadratu w sposób przedstawiony na rysunku. Skorzystaj z założenia indukcyjnego.
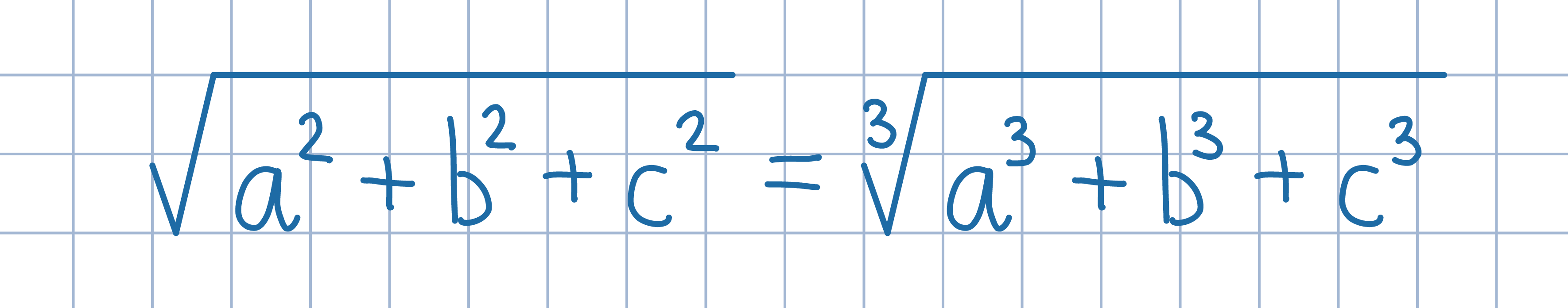 Odp.: (a,b,c) jest równe (x,0,0), (0,x,0) lub (0,0,x), gdzie x jest dowolną liczbą nieujemną.
Odp.: (a,b,c) jest równe (x,0,0), (0,x,0) lub (0,0,x), gdzie x jest dowolną liczbą nieujemną.Oznacz wspólną wartość obu stron równania przez x. Następnie wykonaj poniższe przekształcenia, po czym zbadaj znak wyrażenia stojącego po lewej stronie ostatniej równości.
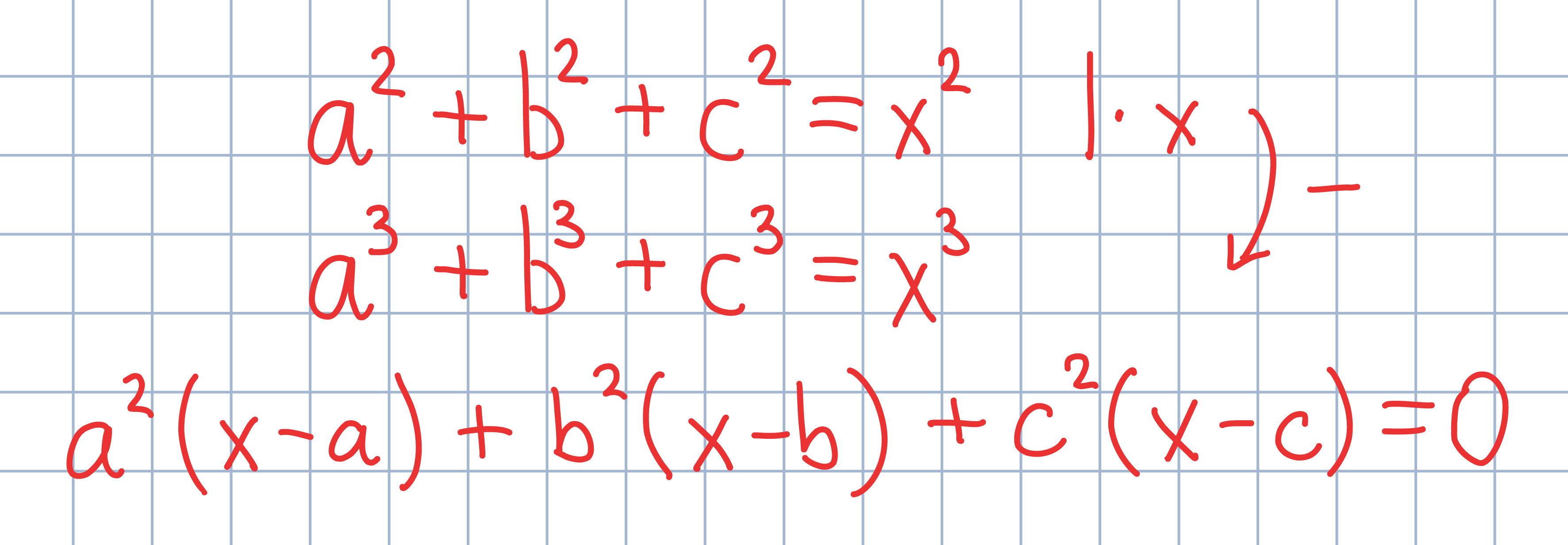
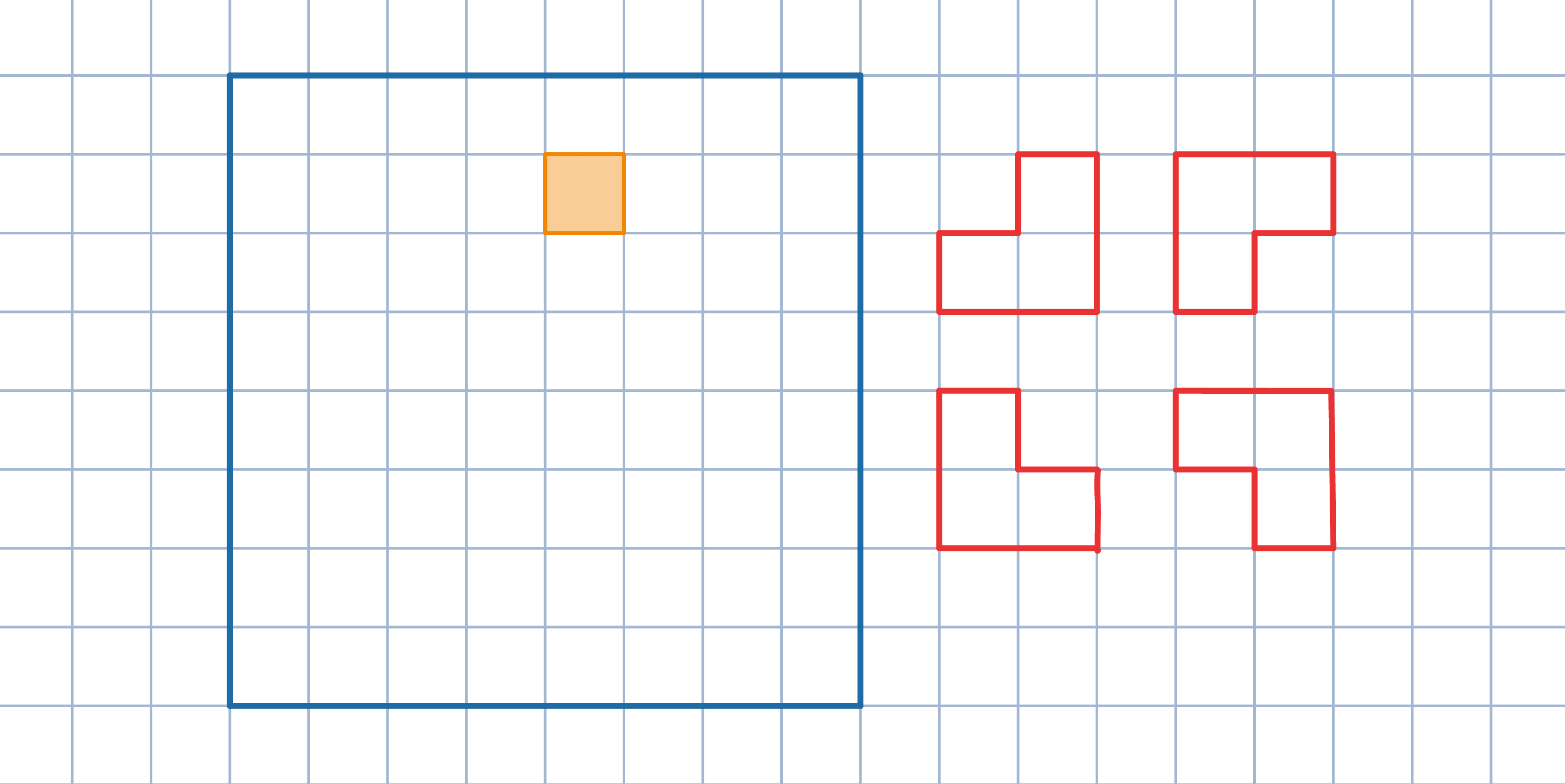
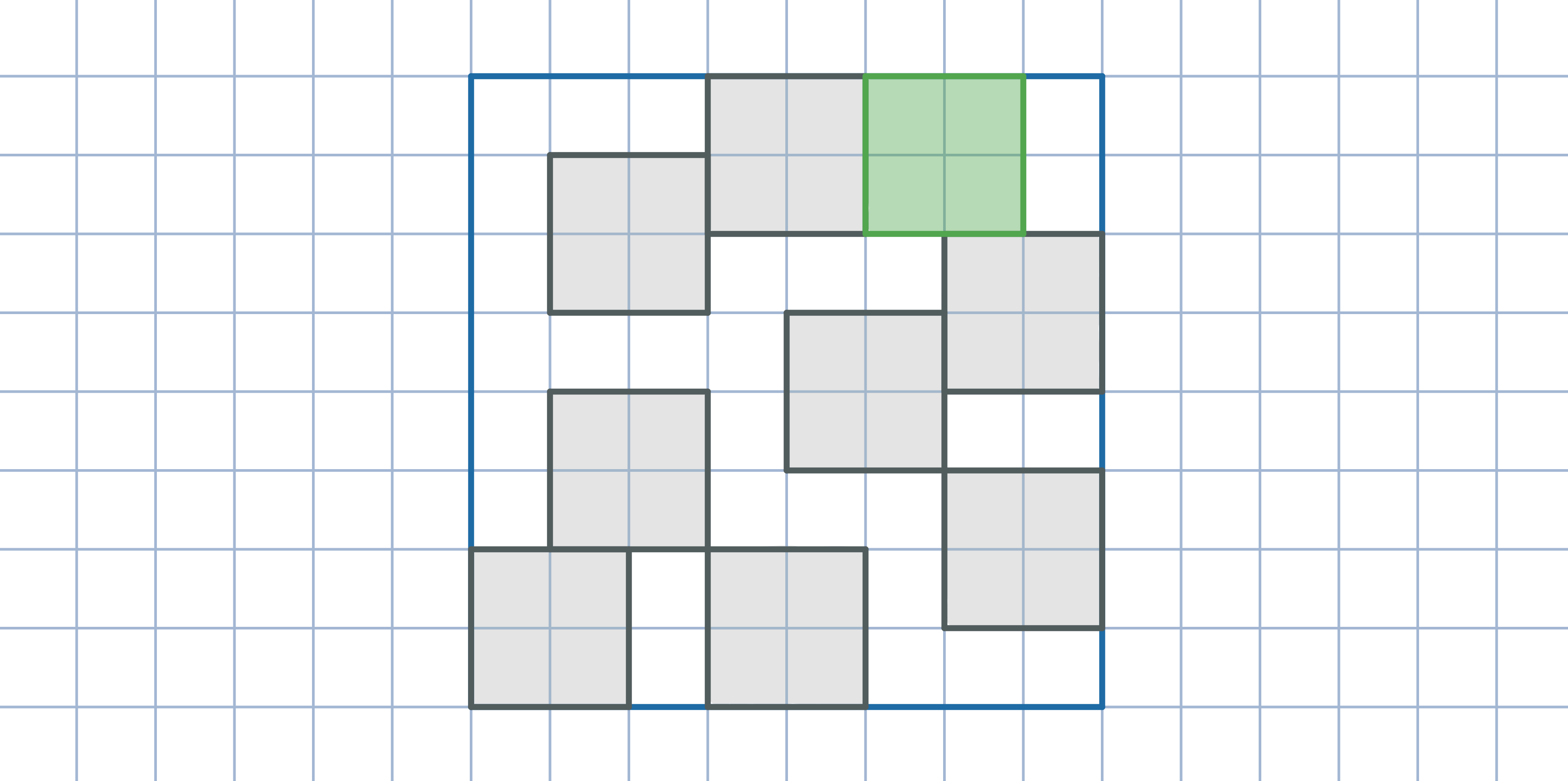 Pokoloruj niektóre pola szachownicy w sposób przedstawiony na rysunku (kolor czerwony). Zauważ, że każdy z umieszczonych na szachownicy kwadratów 2x2 zahacza o wnętrze dokładnie jednego czerwonego kwadratu 2x2.
Pokoloruj niektóre pola szachownicy w sposób przedstawiony na rysunku (kolor czerwony). Zauważ, że każdy z umieszczonych na szachownicy kwadratów 2x2 zahacza o wnętrze dokładnie jednego czerwonego kwadratu 2x2.
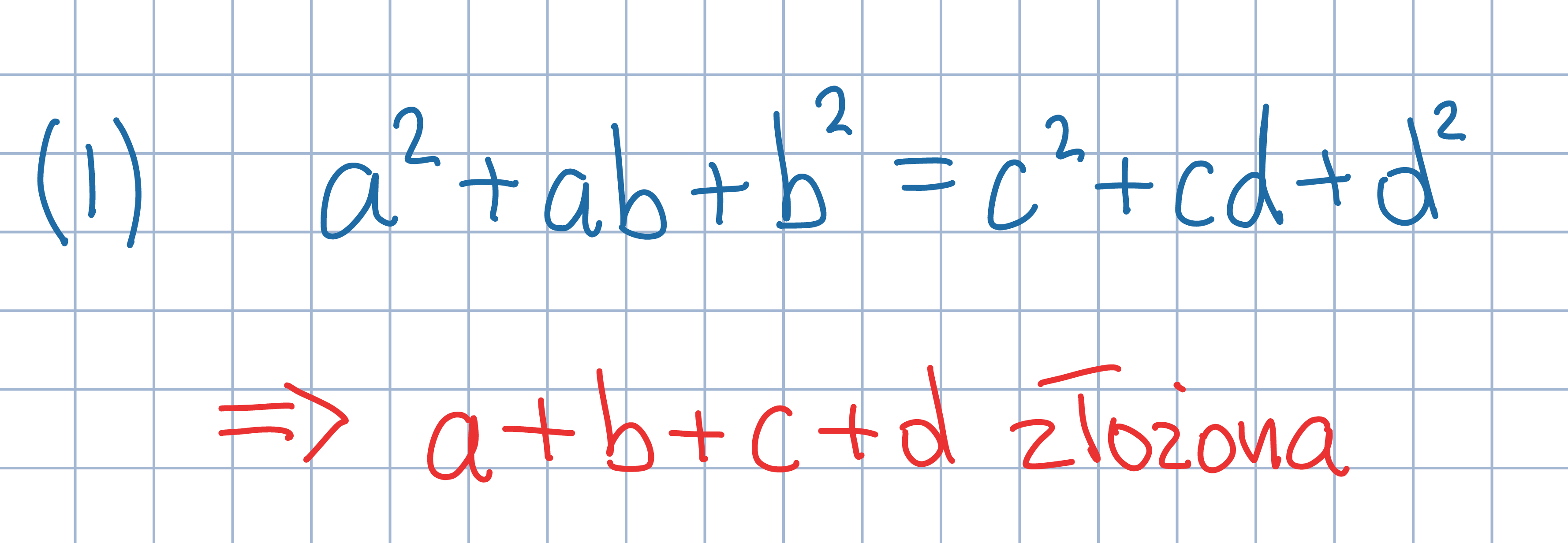 Przekształć zależność (1), doprowadzając ją do poniższej
postaci. Zauważ, że oba czynniki
po prawej stronie są mniejsze od a+b+c+d.
Przekształć zależność (1), doprowadzając ją do poniższej
postaci. Zauważ, że oba czynniki
po prawej stronie są mniejsze od a+b+c+d.
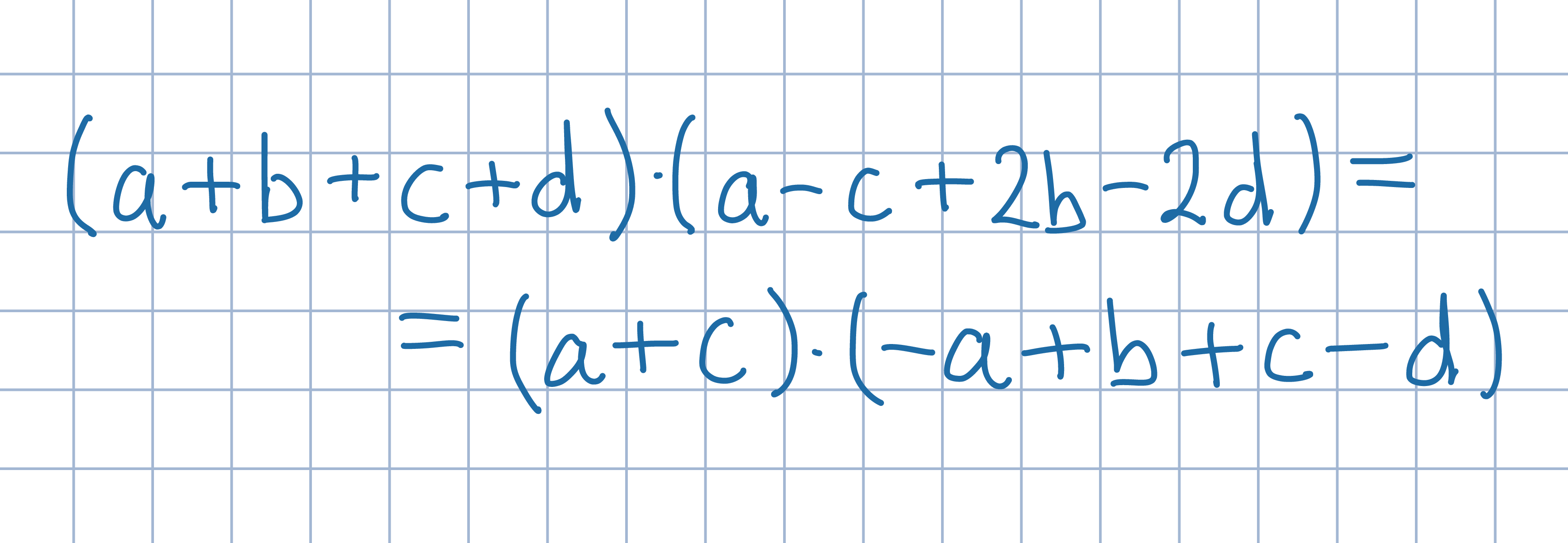
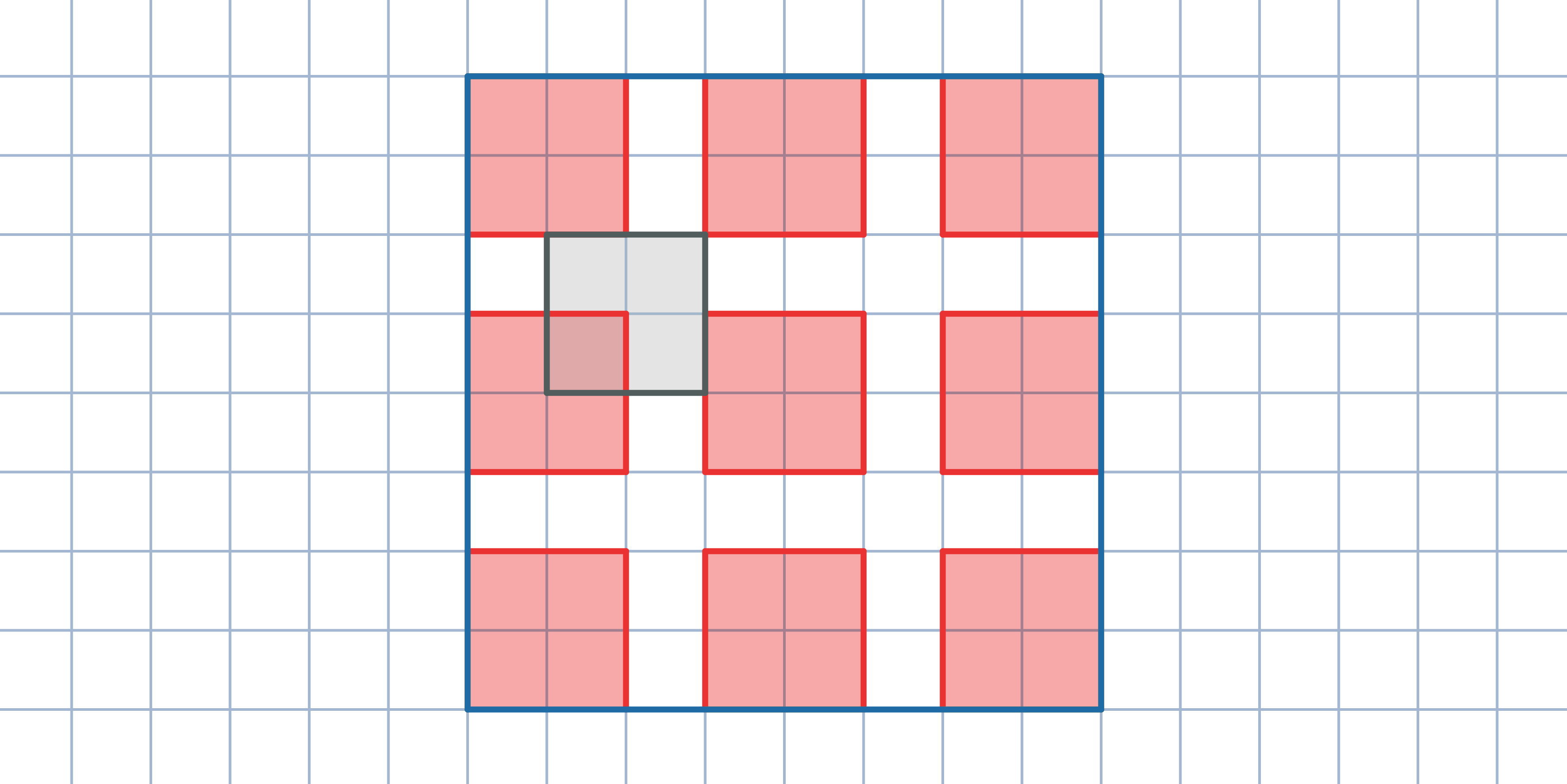
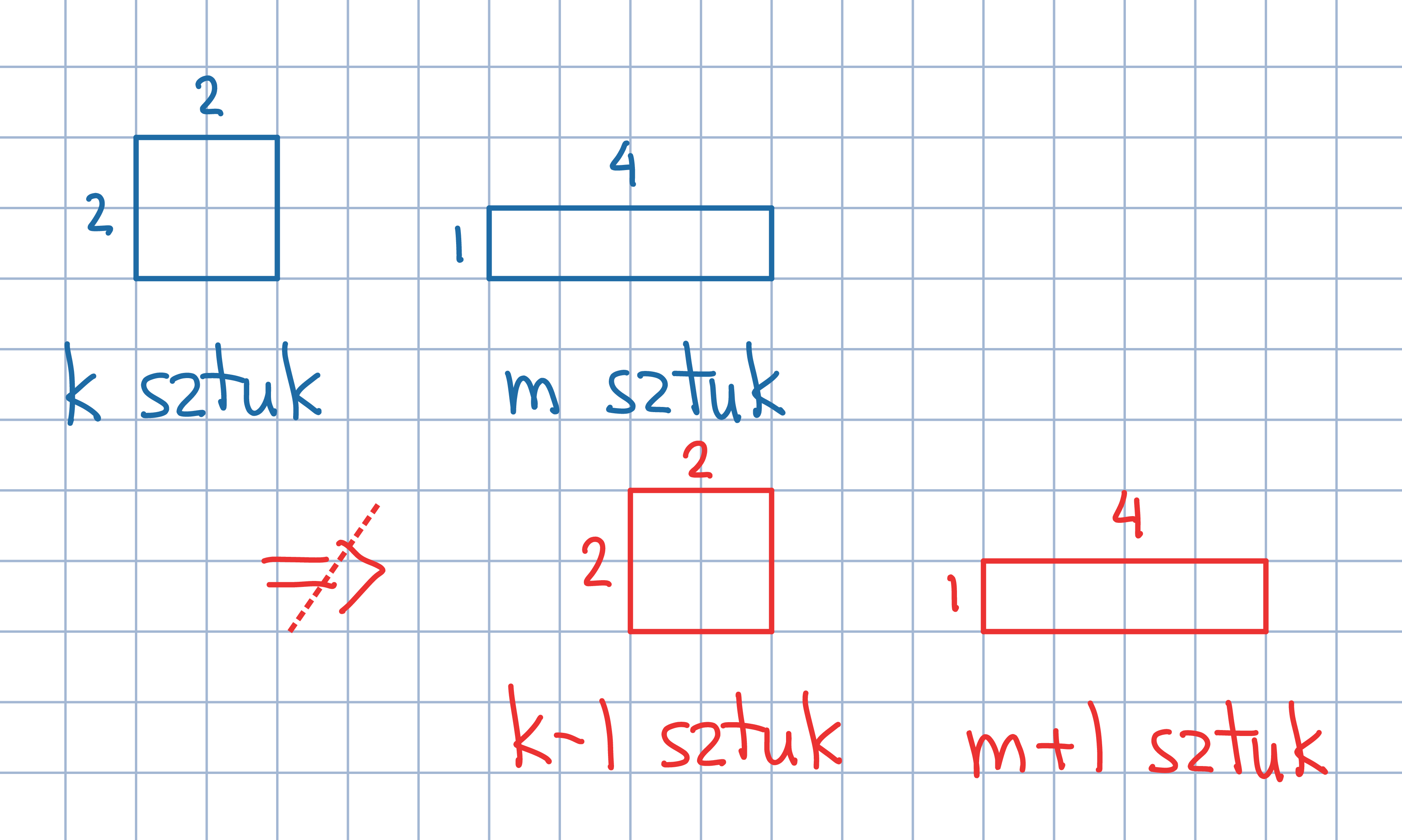 Pokoloruj niektóre pola prostokąta w sposób przedstawiony na rysunku. Zauważ, że każdy klocek 2x2 pokrywa dokładnie 1 pokolorowane pole, a każdy klocek 1x4 pokrywa 0 lub 2 pokolorowane pola.
Pokoloruj niektóre pola prostokąta w sposób przedstawiony na rysunku. Zauważ, że każdy klocek 2x2 pokrywa dokładnie 1 pokolorowane pole, a każdy klocek 1x4 pokrywa 0 lub 2 pokolorowane pola.

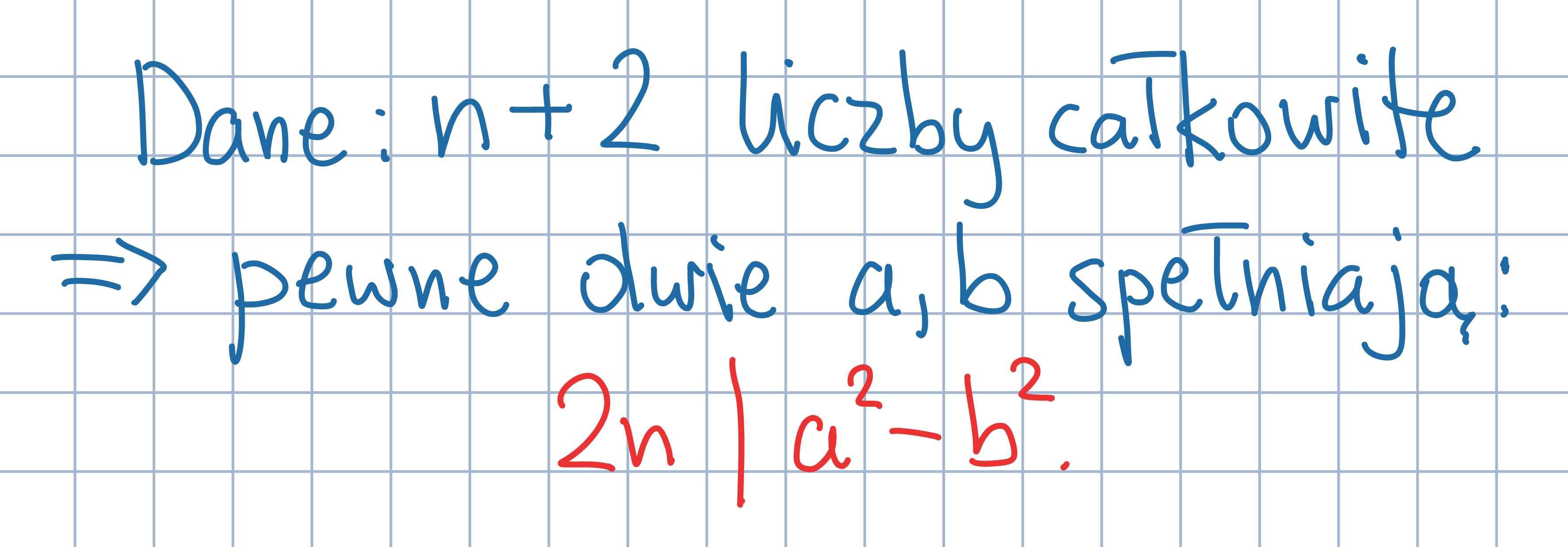 Wszystkie możliwe reszty z dzielenia przez 2n połącz w pary: (0,0),
(1,2n–1), (2,2n–2), ..., (n,n). Uzasadnij, że pewne dwie spośród danych liczb
dają z dzielenia przez 2n reszty znajdujące się w tej samej parze.
Wszystkie możliwe reszty z dzielenia przez 2n połącz w pary: (0,0),
(1,2n–1), (2,2n–2), ..., (n,n). Uzasadnij, że pewne dwie spośród danych liczb
dają z dzielenia przez 2n reszty znajdujące się w tej samej parze.
Najbliższe zajęcia
dla uczniów liceum oraz klas 7-8 szkoły podstawowej
zainteresowanych matematyką