mat edukacja
Uczymy się razem
Konkursy
Konkursy
matematyczne OMJ Olimpiada
Matematyczna
Juniorów OM 2 etap Olimpiada
Matematyczna
2 etap
matematyczne OMJ Olimpiada
Matematyczna
Juniorów OM 2 etap Olimpiada
Matematyczna
2 etap
Przed konkursem matematycznym
Zadania
Zadanie 1–41.
Wyznacz wszystkie dodatnie liczby całkowite, które można przedstawić w postaci sumy liczby pierwszej i liczby złożonej.
Odp.: Szukane liczby to wszystkie liczby naturalne większe od 5.
Zauważ, że każda liczba parzysta jest sumą liczby 2 oraz
liczby parzystej. Poszukaj podobnego rozkładu dla liczb nieparzystych.
Zadanie 1–40.
W pewnej szkole jest 100 uczniów. Języka hiszpańskiego uczy się 60 uczniów, francuskiego — 70, niemieckiego — 80, a angielskiego — 91. Wykaż, że pewna osoba w szkole uczy się wszystkich czterech języków.
Przypuśćmy, że każdy uczeń uczy się co najwyżej trzech języków i każdy z nich ma po jednym zeszycie do każdego z tych przedmiotów. Jaka jest maksymalna łączna liczba wszystkich zeszytów?
Zadanie 1–39.
Na poniższym rysunku dane są dwa kwadraty o wspólnym wierzchołku. Odcinki żółte mają długości a i b, a zielony długość c. Wykaż, że a+b ≥ c .
Uzasadnij, że długość żółtego przerywanego odcinka jest równa a. W tym celu poszukaj trójkątów przystających.
Zadanie 1–38.
W poniższym dodawaniu różnym literom odpowiadają różne cyfry, a takim samym literom — takie same cyfry. Czy taki zapis dodawania jest możliwy?
Odp. Taki zapis dodawania nie jest możliwy.
Uzasadnij najpierw, że E=T+1, a następnie, że E+E=10+T. Doprowadź do sprzeczności,
przyglądając się drugiej kolumnie dodawania (od prawej strony).
Zadanie 1–37.
Wykaż, że liczba złożona z 91 jedynek jest złożona.
Uzasadnij, że liczba ta jest podzielna przez 1111111 (7 jedynek). Może się przydać równość 91=7∙13.
Zadanie 1–36.
Dany jest trapez ABCD o podstawach AB i CD. Przekątne tego trapezu przecinają się w punkcie E. Oznaczmy przez S, T oraz W odpowiednio pola trójkątów ABE, CDE oraz trapezu ABCD. Wykaż, że √S+√T=√W.
Oznacz przez a, b odpowiednio długości podstaw AB, CD, a przez c długość wysokości trójkąta ABE opuszczonej z wierzchołka E. Wyznacz długość wysokości trójkąta CDE poprowadzonej z wierzchołka E.
Zadanie 1–35.
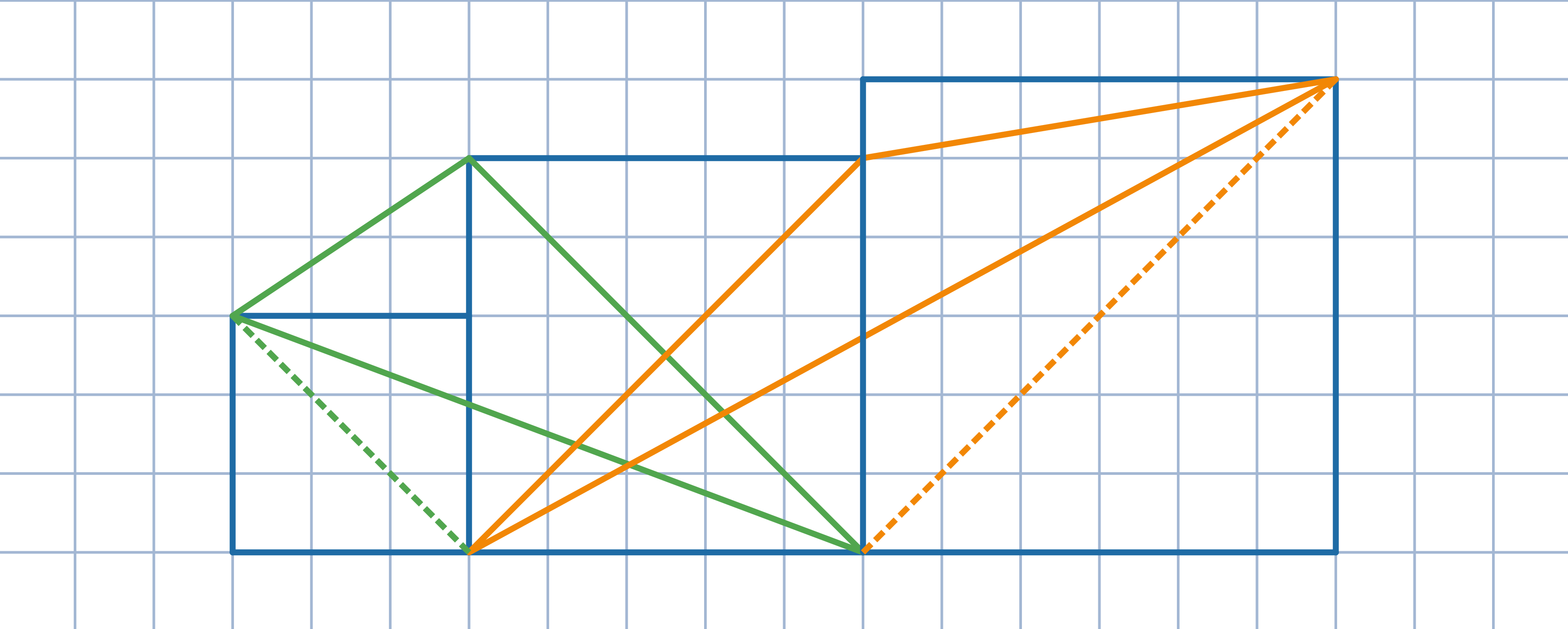
Przez punkt leżący wewnątrz kwadratu poprowadzono proste prostopadłe, które dzielą kwadrat na 4 czworokąty A, B, C, D, w sposób przedstawiony na rysunku. Wykaż, że suma obwodów czworokątów A i C jest równa sumie obwodów czworokątów B i D.
Uzasadnij, że suma długości odcinków zielonego i żółtego jest równa sumie długości odcinków czerwonego i niebieskiego.
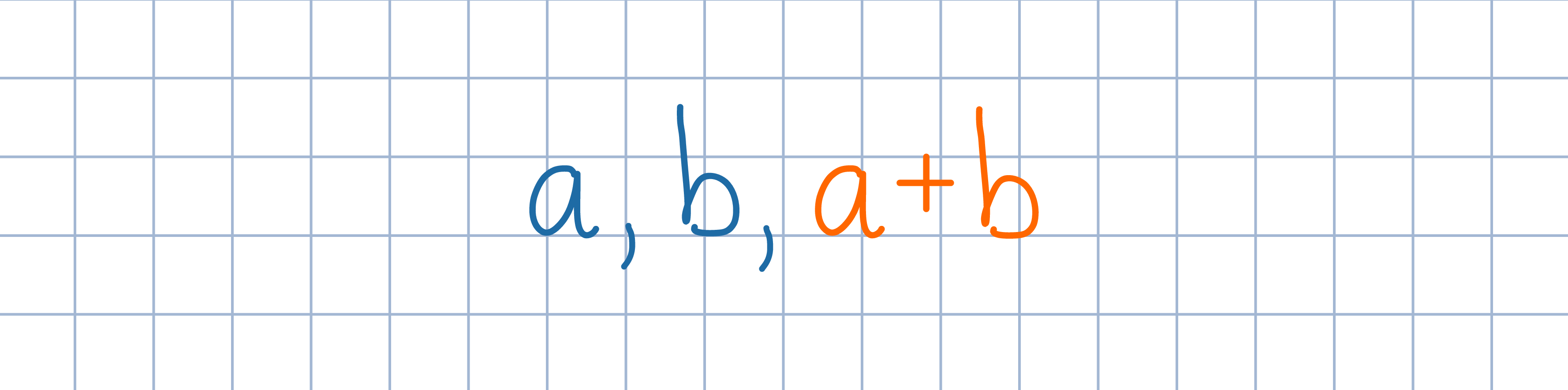 Odp.:
Na tablicy napisno dwie liczby (a,0) lub trzy liczby (a,-a,0), gdzie a jest dowolną liczbą różną od 0.
Odp.:
Na tablicy napisno dwie liczby (a,0) lub trzy liczby (a,-a,0), gdzie a jest dowolną liczbą różną od 0.Uzasadnij, że suma pewnych dwóch (różnych od 0) liczb napisanych na tablicy i mających ten sam znak nie może być zapisana na tablicy.
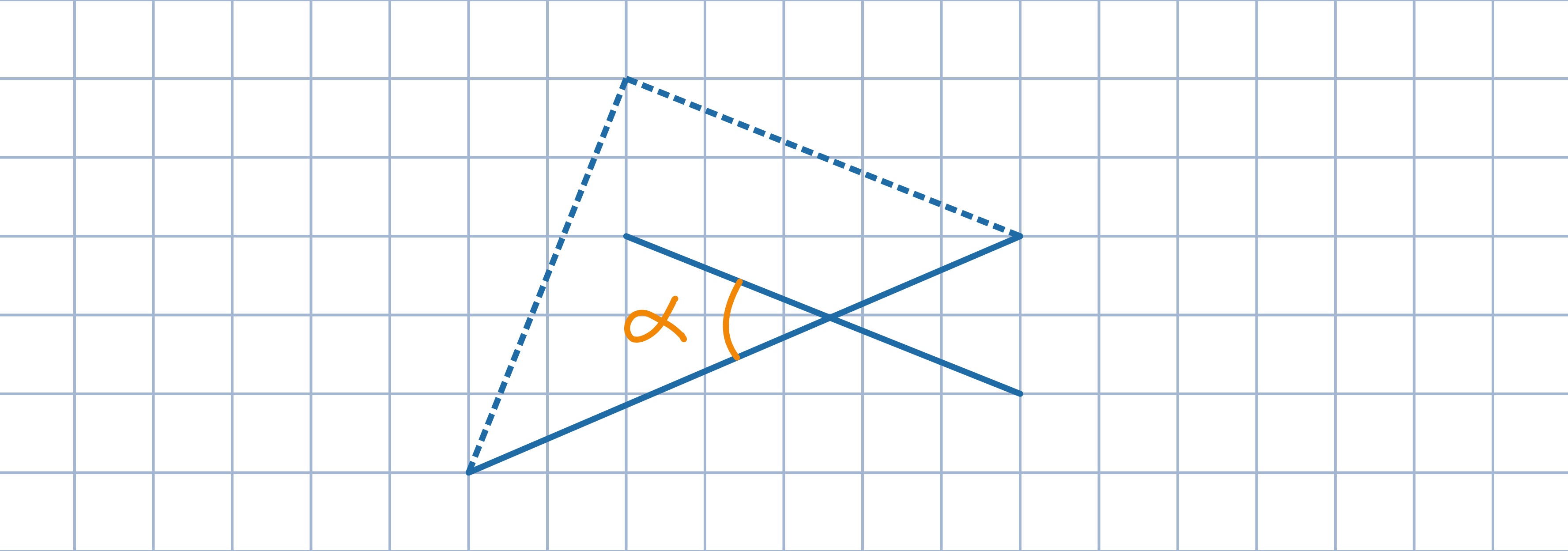
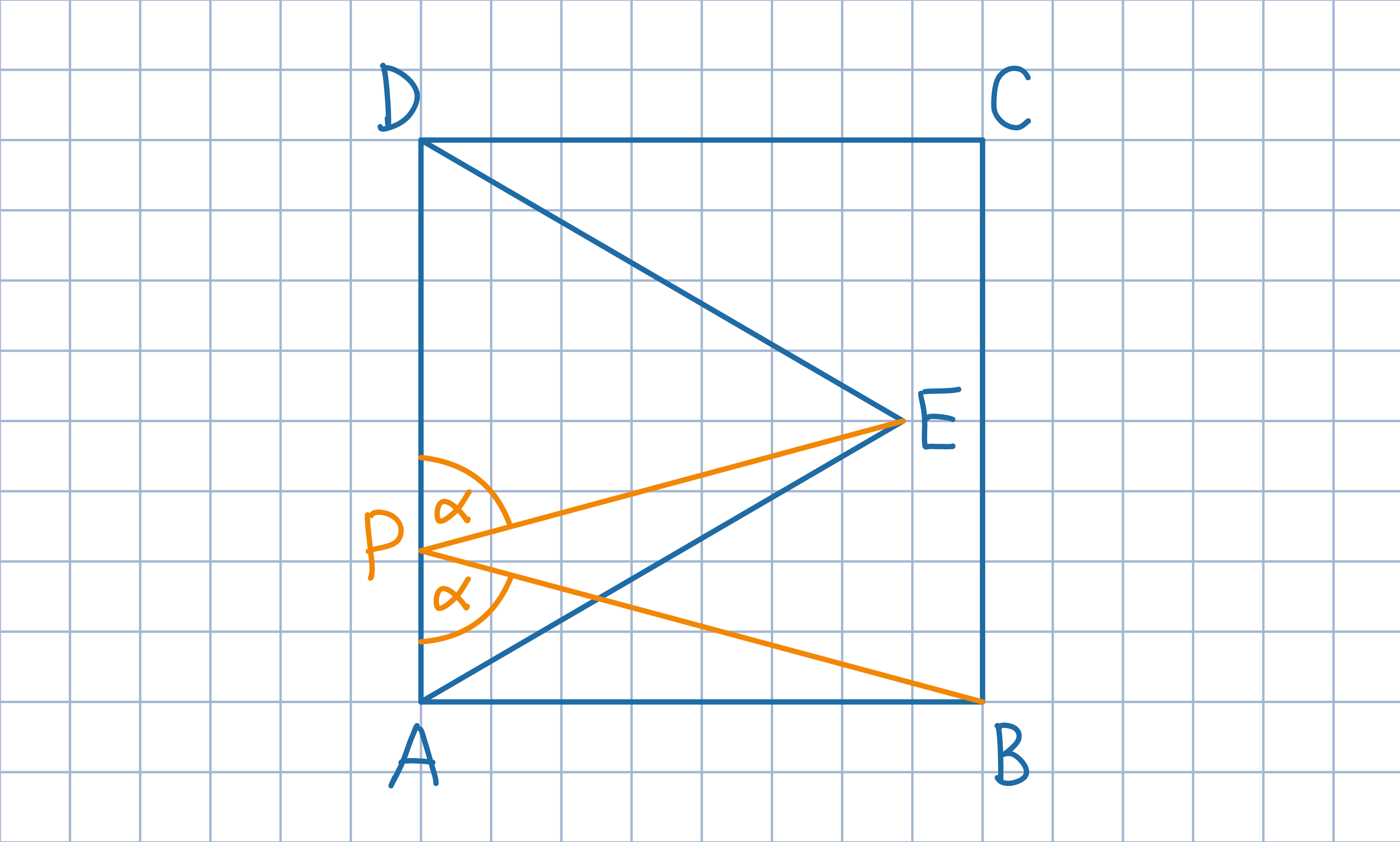 Odp.: α=75°.
Odp.: α=75°.Oznacz przez F punkt symetryczny do punktu E względem prostej AD. Uzasadnij, że punkt P leży na odcinku BF. Następnie wyznacz miary kątów trójkąta ABF.

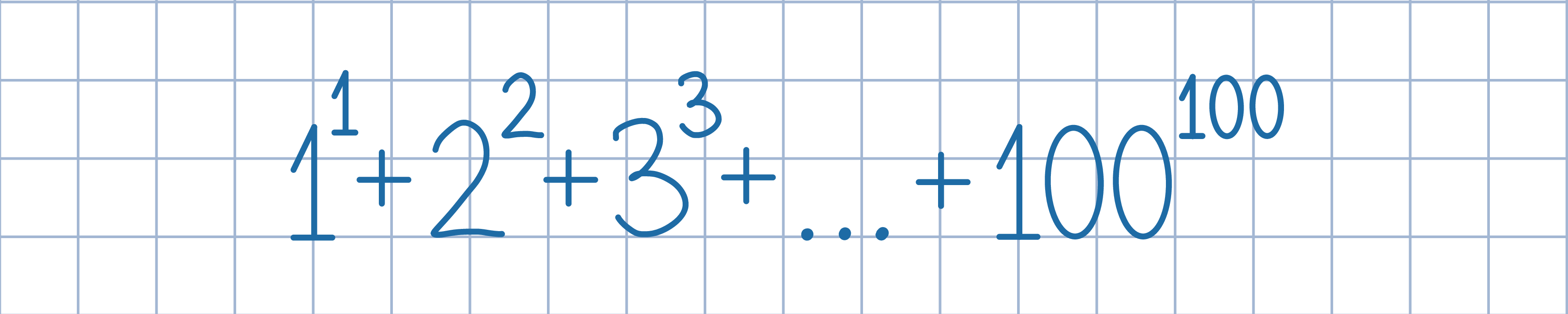 Odp.: n=201.
Odp.: n=201.Zauważ, że liczba 1^1+2^2+3^3+...+99^99 jest mniejsza od 99∙99^99. Wywnioskuj stąd, że wyjściowa liczba jest mniejsza od 2∙100^100.
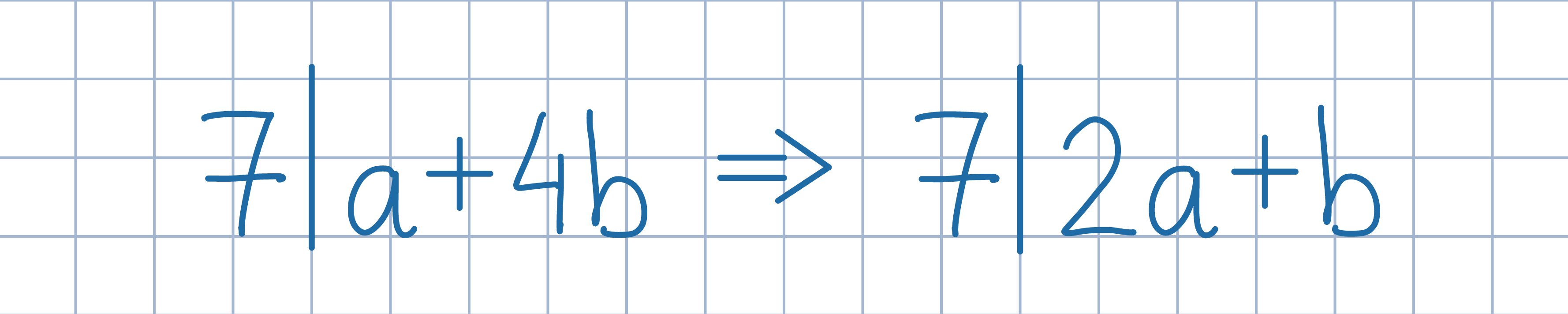
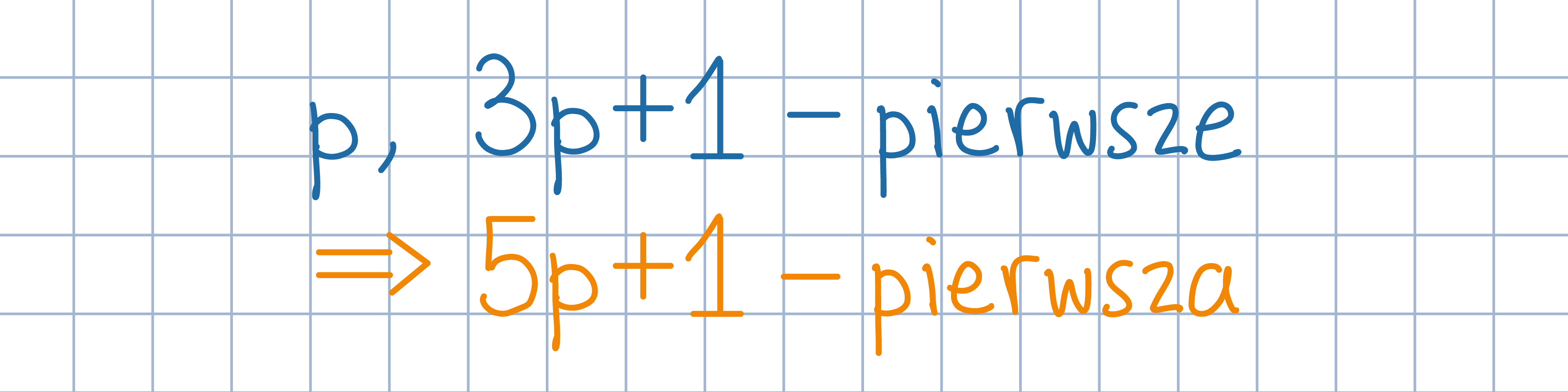 Uzasadnij, że jedna z liczb p lub 3p+1 jest parzysta.
Uzasadnij, że jedna z liczb p lub 3p+1 jest parzysta.
 Liczbę a przedstaw w postaci 10∙k+c, gdzie k jest pewną liczbą
Liczbę a przedstaw w postaci 10∙k+c, gdzie k jest pewną liczbą 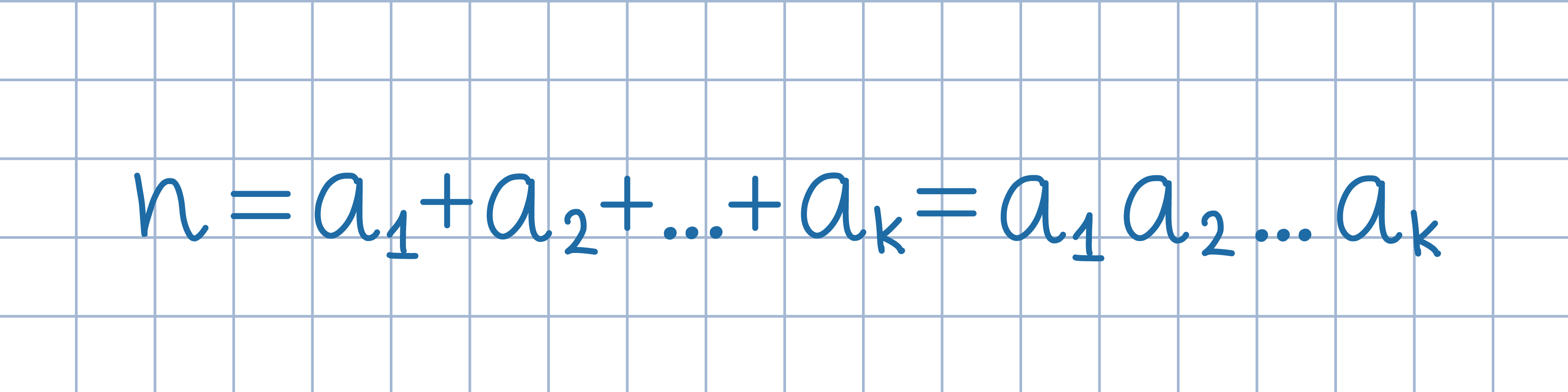 Odp. Warunki zadania spełniają wszystkie liczby złożone n.
Odp. Warunki zadania spełniają wszystkie liczby złożone n.Liczbę złożoną n przestaw w postaci iloczynu dwóch liczb naturalnych p, q większych od 1, po czym pomnóż ten iloczyn przez odpowiednią liczbę jedynek.
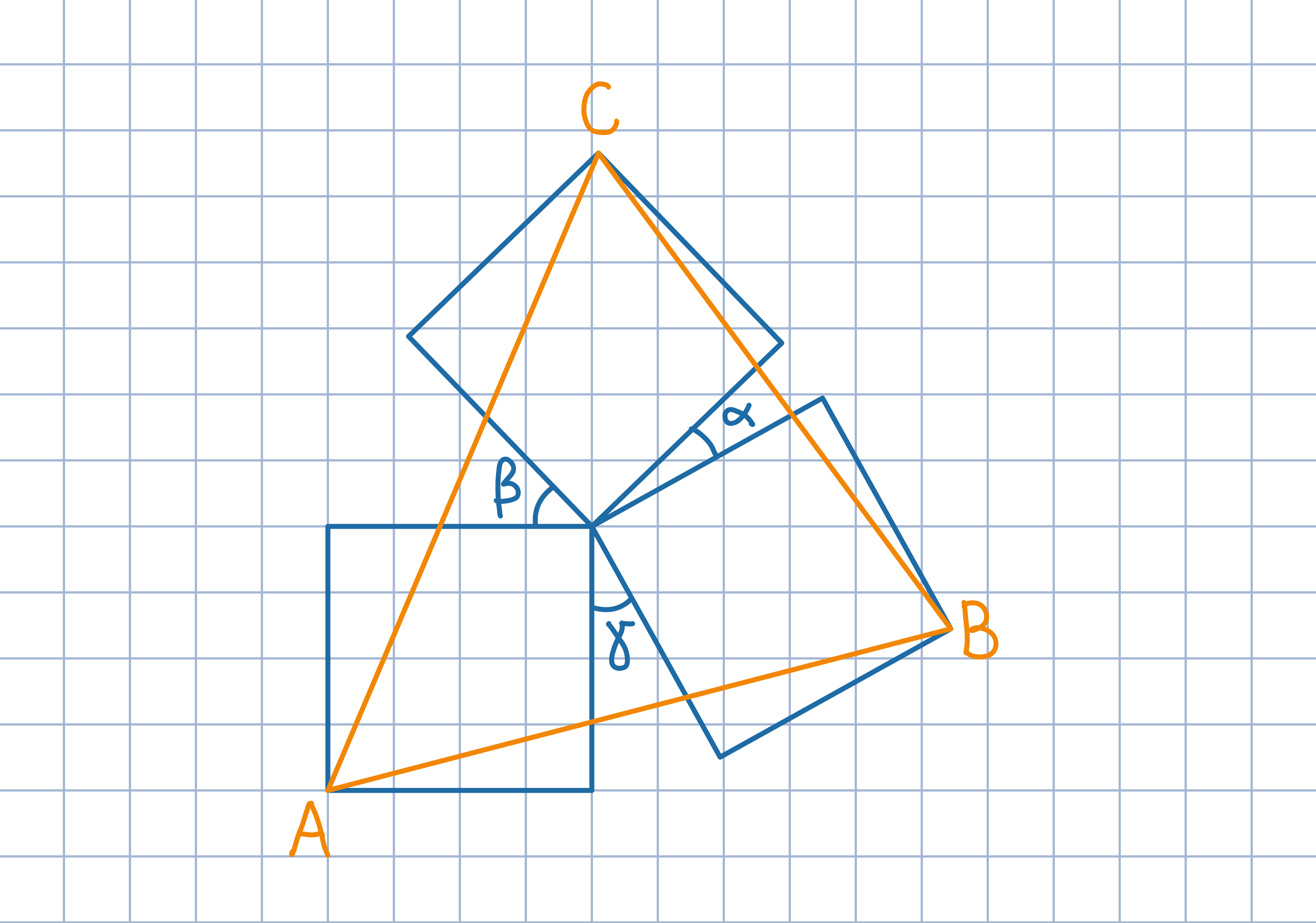 Odp. Miary kątów trójkąta ABC przy wierzchołkach
A, B, C są równe odpowiednio
Odp. Miary kątów trójkąta ABC przy wierzchołkach
A, B, C są równe odpowiednio Zauważ, że odległości od wspólnego wierzchołka trzech kwadratów do punktów A, B, C są równe.
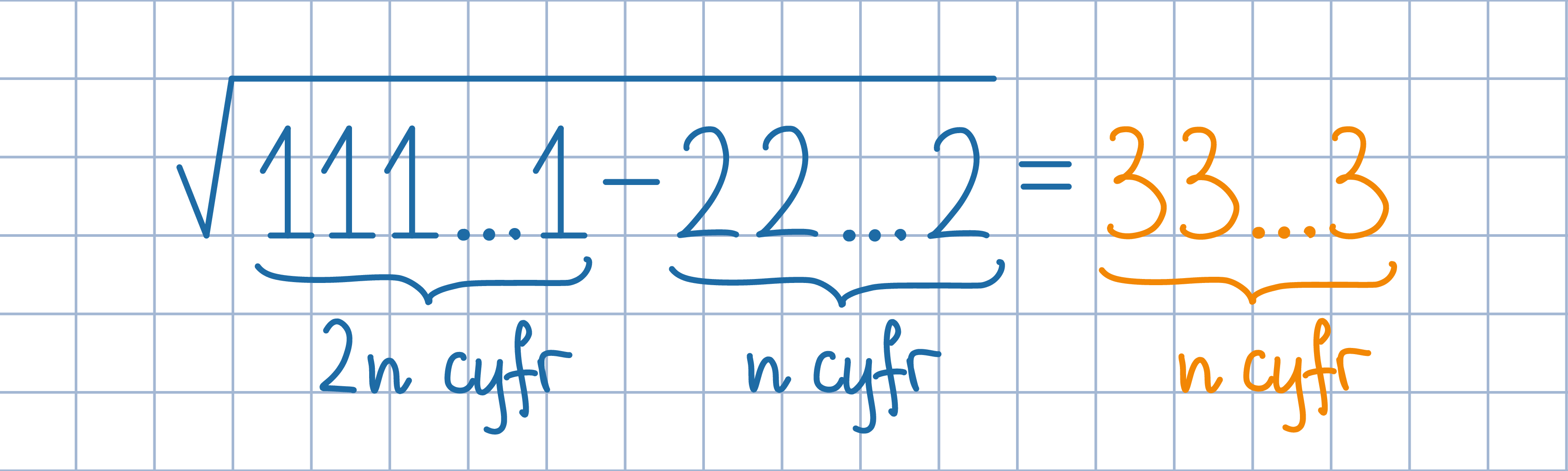 Zauważ, że liczba 111...1 (2n jedynek) jest równa (10^(2n)-1)/9. Zapisz pozostałe
dwie liczby w analogiczny sposób.
Zauważ, że liczba 111...1 (2n jedynek) jest równa (10^(2n)-1)/9. Zapisz pozostałe
dwie liczby w analogiczny sposób.
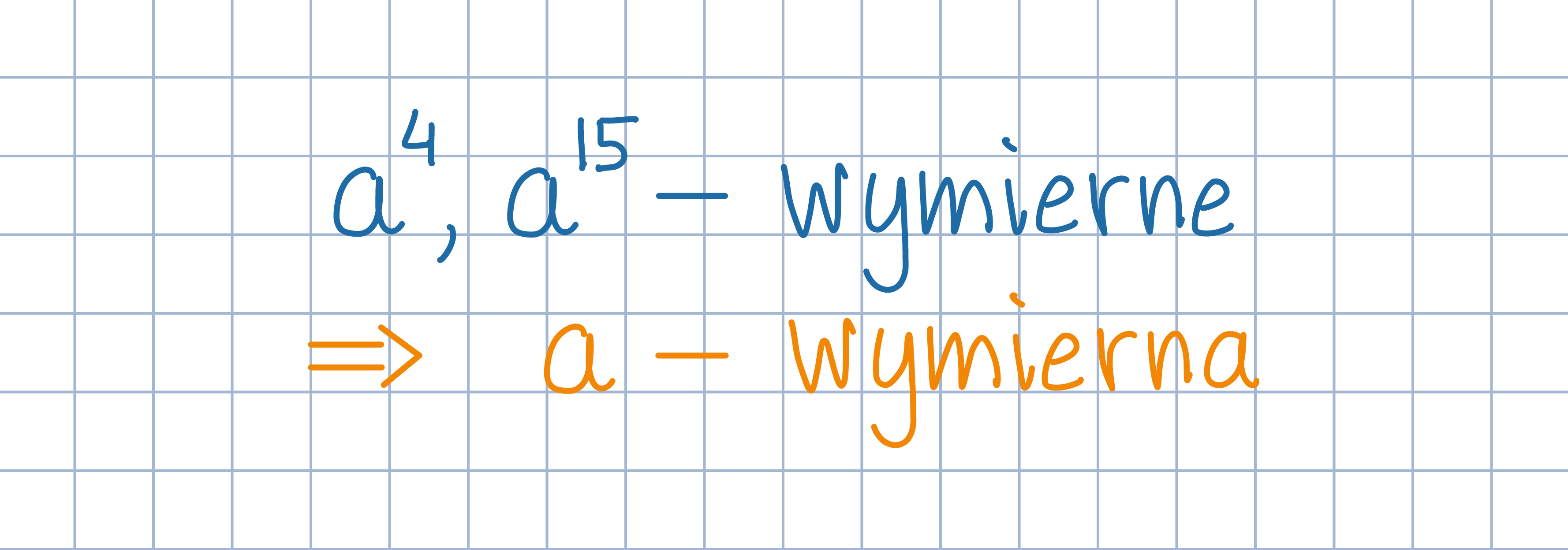

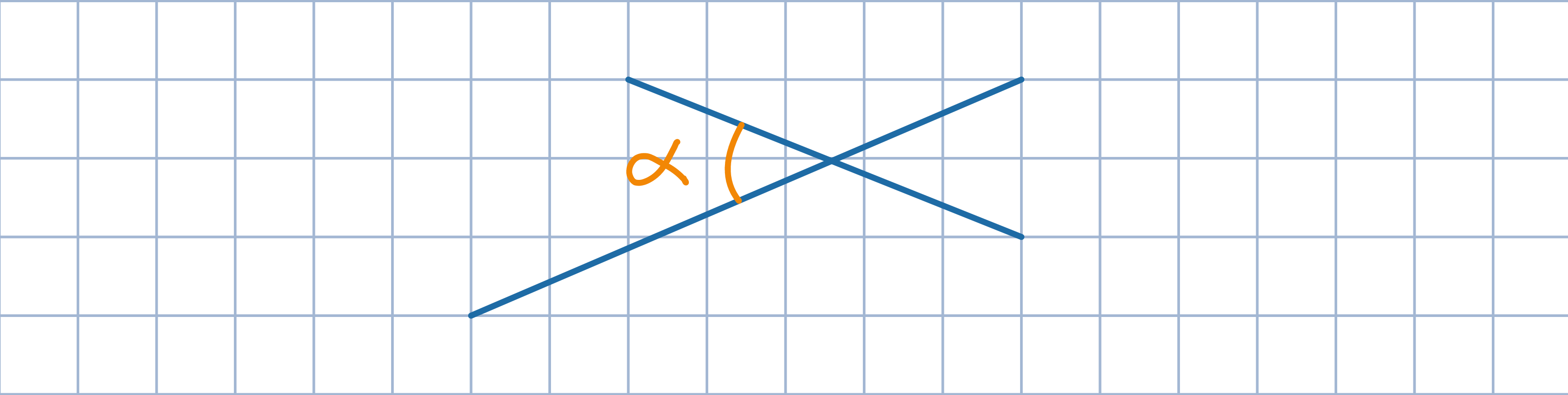
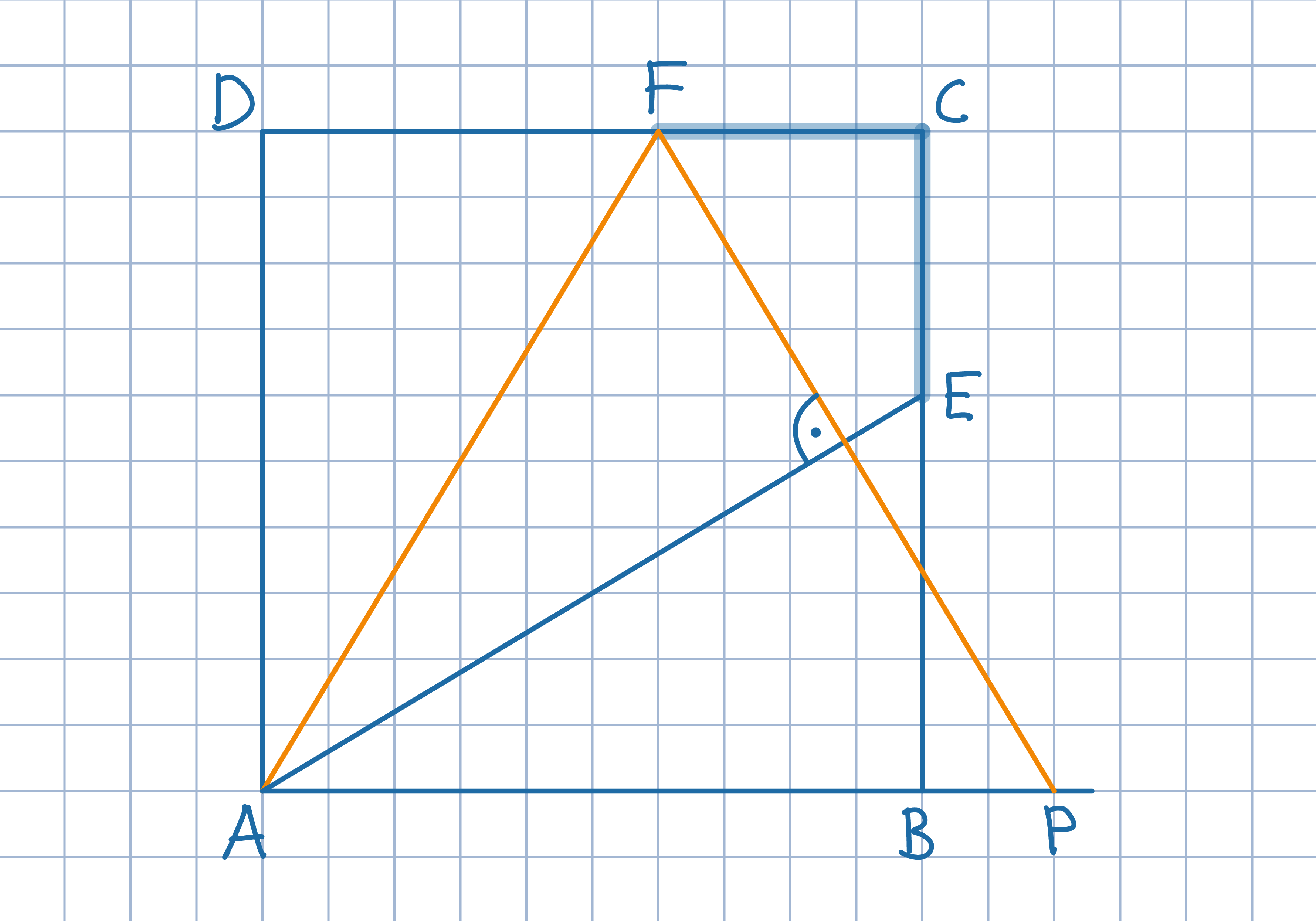 Uzasadnij, że zaznaczone na rysunku kąty są równe.
Uzasadnij, że zaznaczone na rysunku kąty są równe.
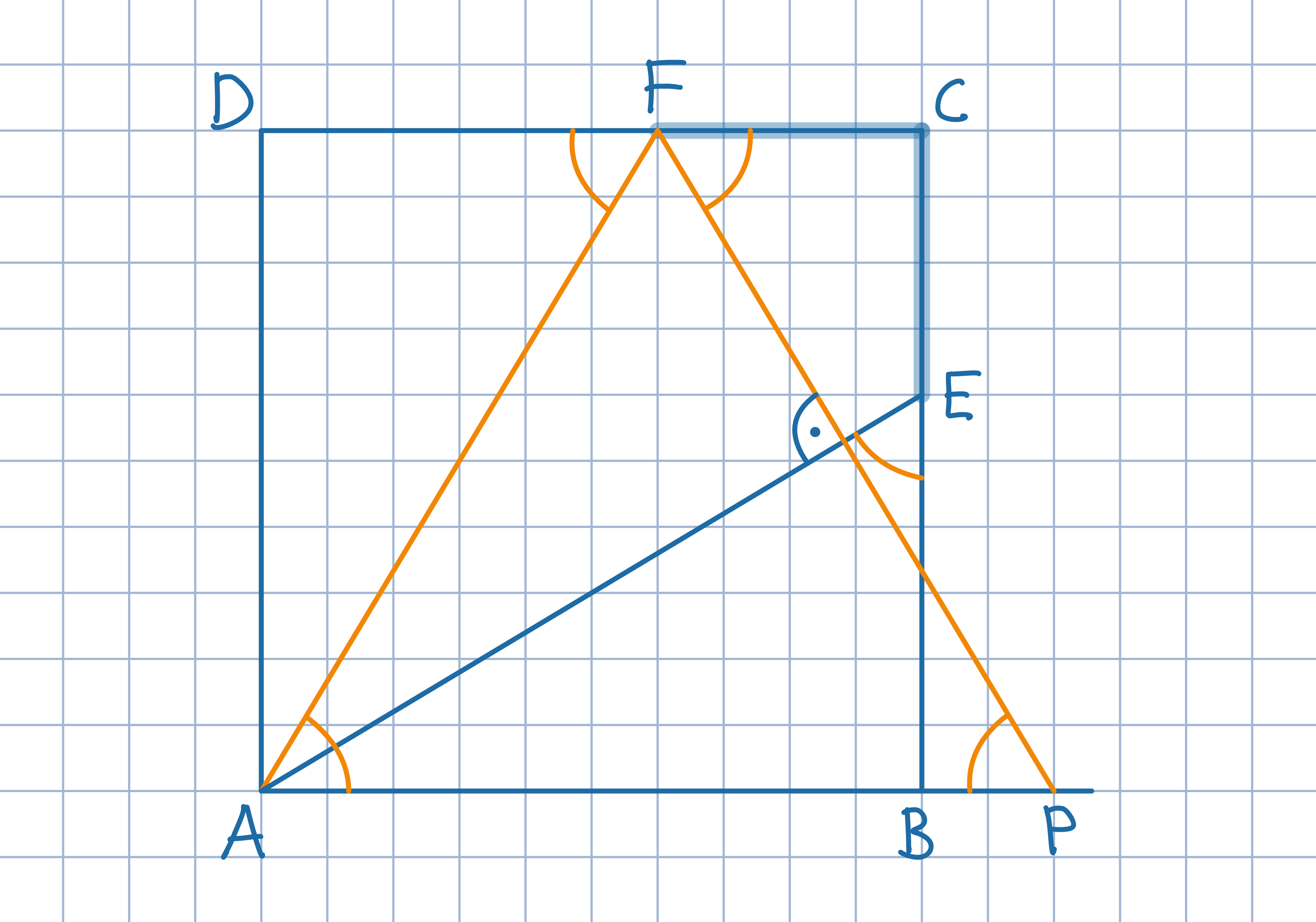
 Pomnóż dany iloczyn z lewej strony przez
Pomnóż dany iloczyn z lewej strony przez 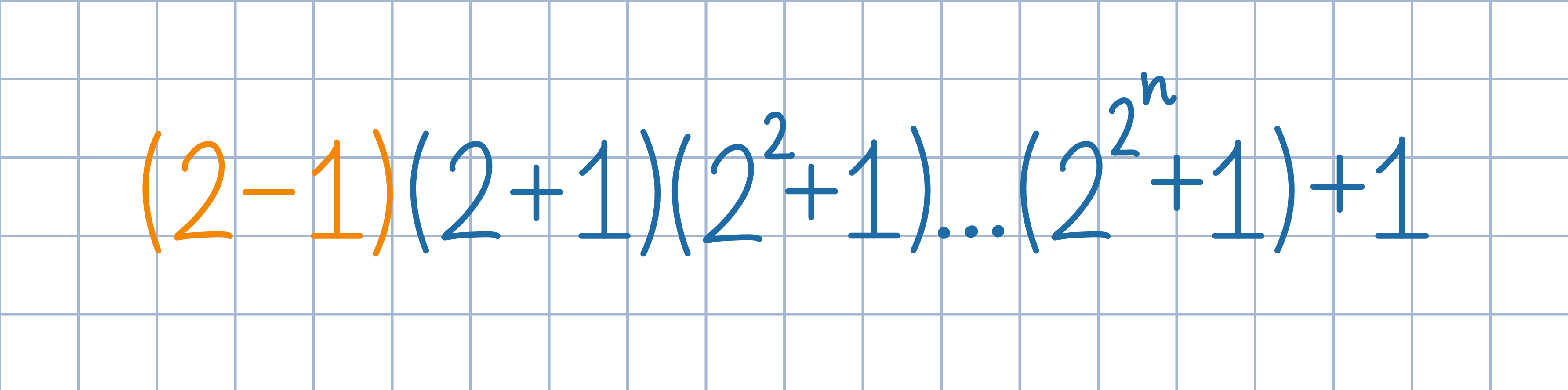
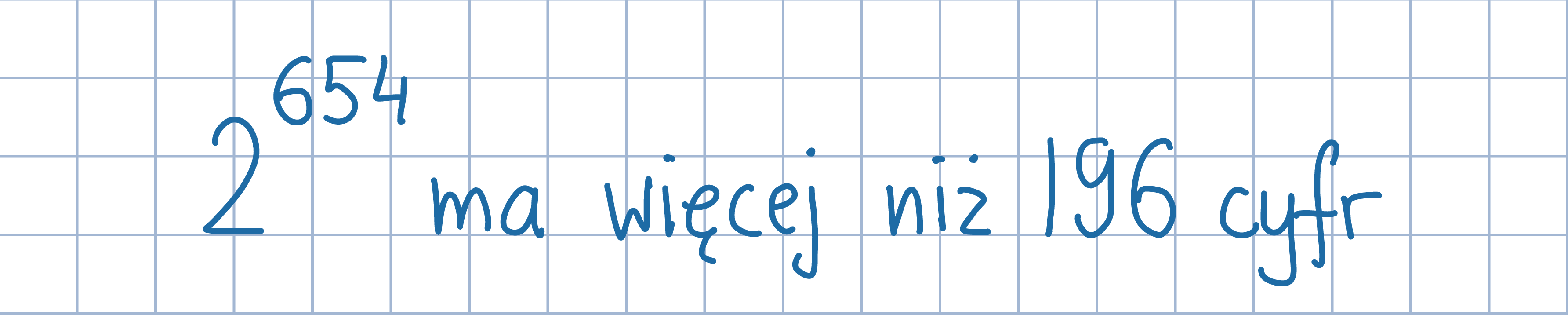 Zapisz daną liczbę w poniższej postaci. Zauważ, że 2^10=1024>10^3.
Zapisz daną liczbę w poniższej postaci. Zauważ, że 2^10=1024>10^3.

 Podnieś obie strony dowodzonej nierówności do kwadratu.
Pamiętaj o twierdzeniu Pitagorasa oraz wzorach na pole trójkąta.
Podnieś obie strony dowodzonej nierówności do kwadratu.
Pamiętaj o twierdzeniu Pitagorasa oraz wzorach na pole trójkąta.
 Uzasadnij najpierw, że każda liczba złożona mniejsza od 30 dzieli się przez 2, 3 lub 5.
Uzasadnij najpierw, że każda liczba złożona mniejsza od 30 dzieli się przez 2, 3 lub 5.
 Odp.: 24 km/h.
Odp.: 24 km/h.Oznacz przez a długość trasy rowerzysty (w kilometrach) w jedną stroną. Ile godzin jechał rowerzysta w każdą ze stron?
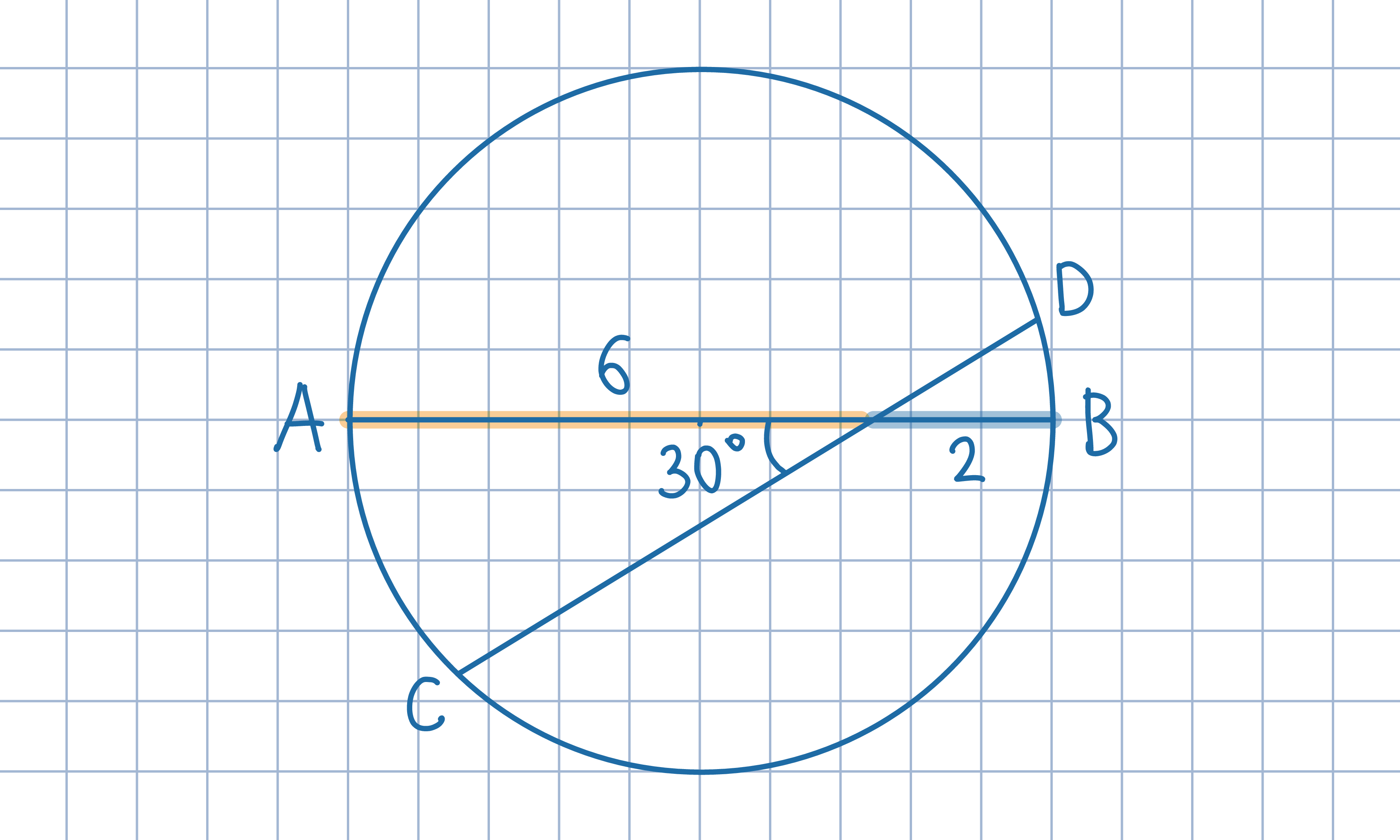 Oblicz najpierw promień okręgu, a następnie odległość środka okręgu od cięciwy CD.
Oblicz najpierw promień okręgu, a następnie odległość środka okręgu od cięciwy CD.
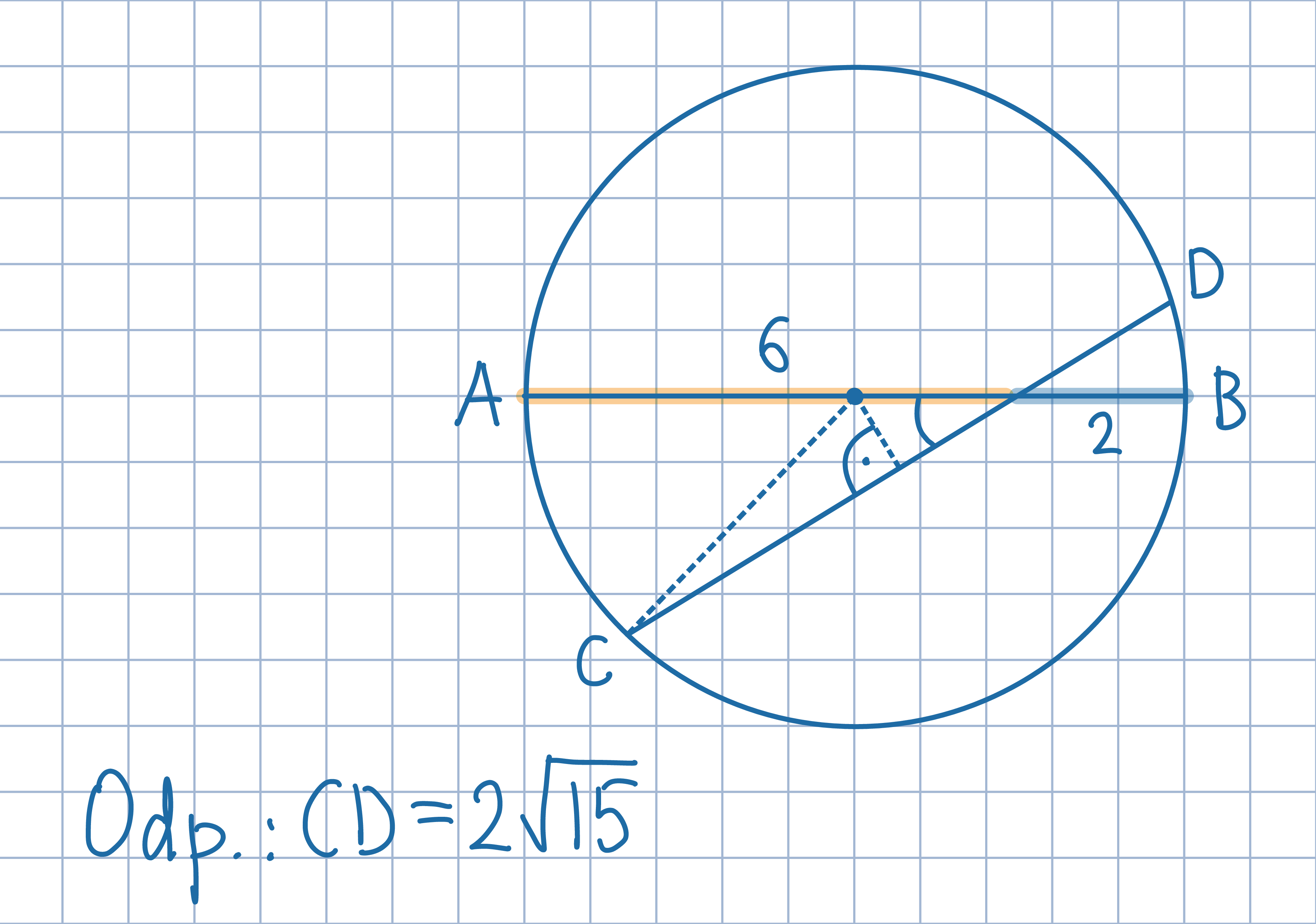
 Odp.: Jedyną taką liczbą jest p=3.
Odp.: Jedyną taką liczbą jest p=3.Uzasadnij, że jeśli liczba p nie jest podzielna przez 3, to liczba p^2+2 jest podzielna przez 3.
 Przekształć najpierw dane wyrażenie do
poniższej postaci. Uzasadnij następnie, że pewien z czterech otrzymanych czynników jest podzielny przez 3 i pewien jest podzielny przez 5. Następnie zauważ, że jeśli n jest liczbą nieparzystą, to jeden
z czynników n–1 lub n+1 jest podzielny przez 4.
Przekształć najpierw dane wyrażenie do
poniższej postaci. Uzasadnij następnie, że pewien z czterech otrzymanych czynników jest podzielny przez 3 i pewien jest podzielny przez 5. Następnie zauważ, że jeśli n jest liczbą nieparzystą, to jeden
z czynników n–1 lub n+1 jest podzielny przez 4.
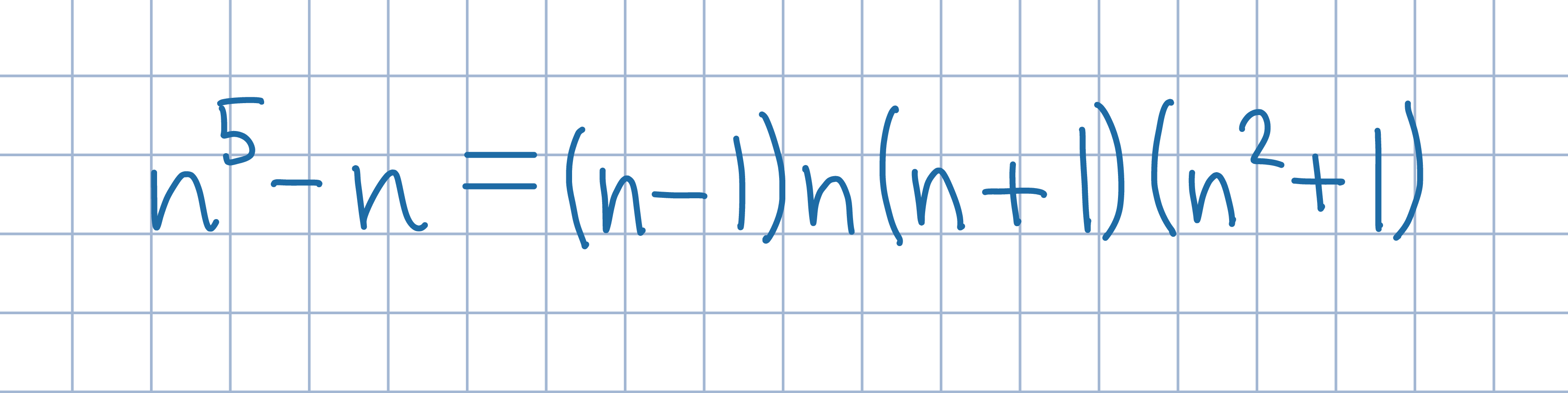
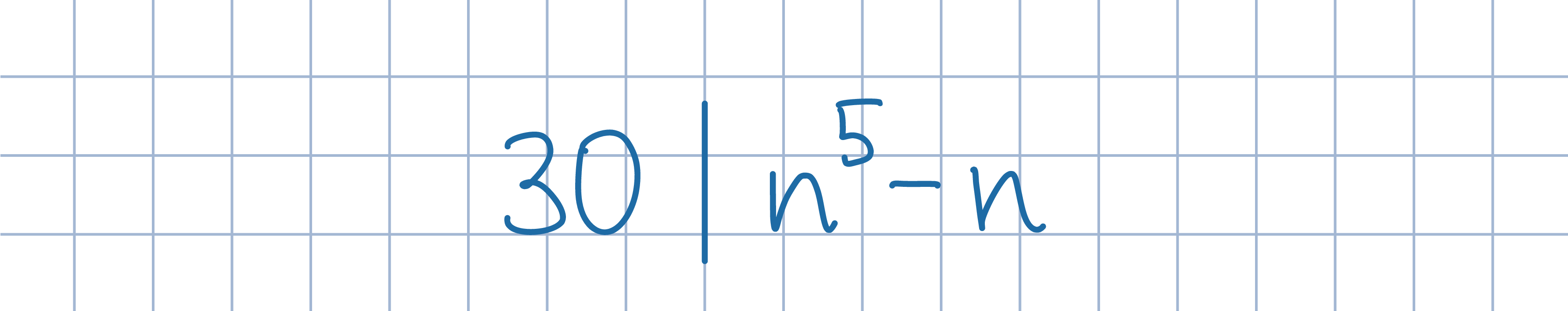 Przekształć najpierw dane wyrażenie do
poniższej postaci. Uzasadnij następnie, że pewien z czterech otrzymanych czynników jest podzielny przez 2, pewien przez 3, a także pewien przez 5.
Przekształć najpierw dane wyrażenie do
poniższej postaci. Uzasadnij następnie, że pewien z czterech otrzymanych czynników jest podzielny przez 2, pewien przez 3, a także pewien przez 5.
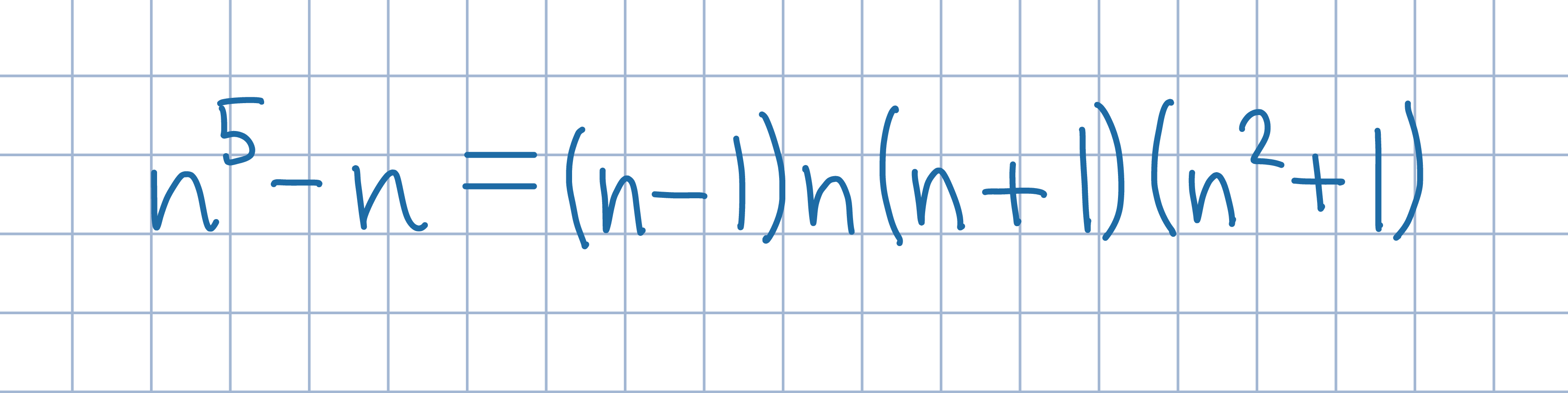
 Odp.: ab/2.
Odp.: ab/2.

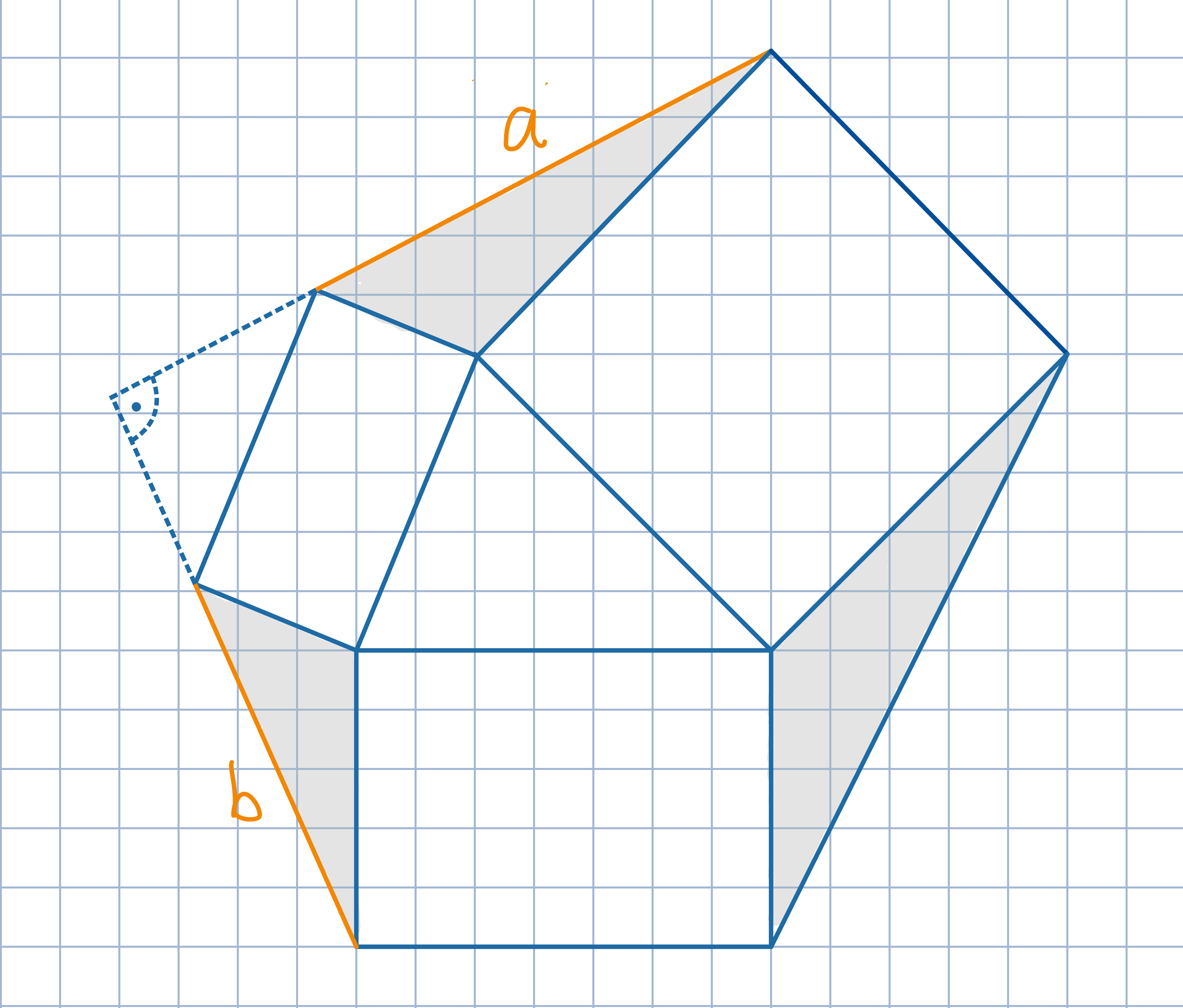
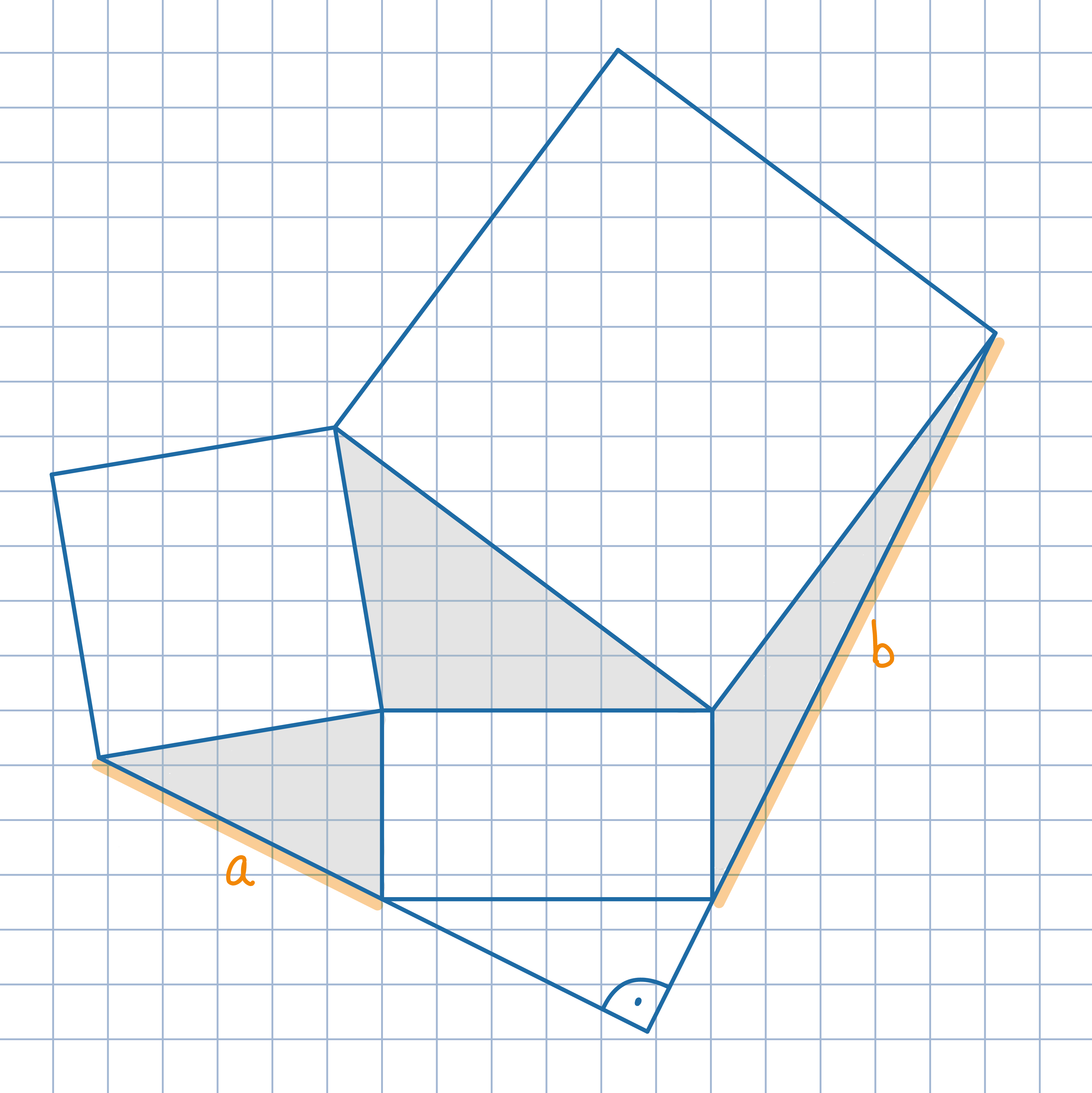 Odp.: ab/2.
Odp.: ab/2.Obróć dwa trójkąty w sposób przedstawiony na rysunku, sklejając wszystkie szare trójkąty ze sobą. Uzasadnij, że powstał w ten sposób trójkąt i jest on prostokątny.

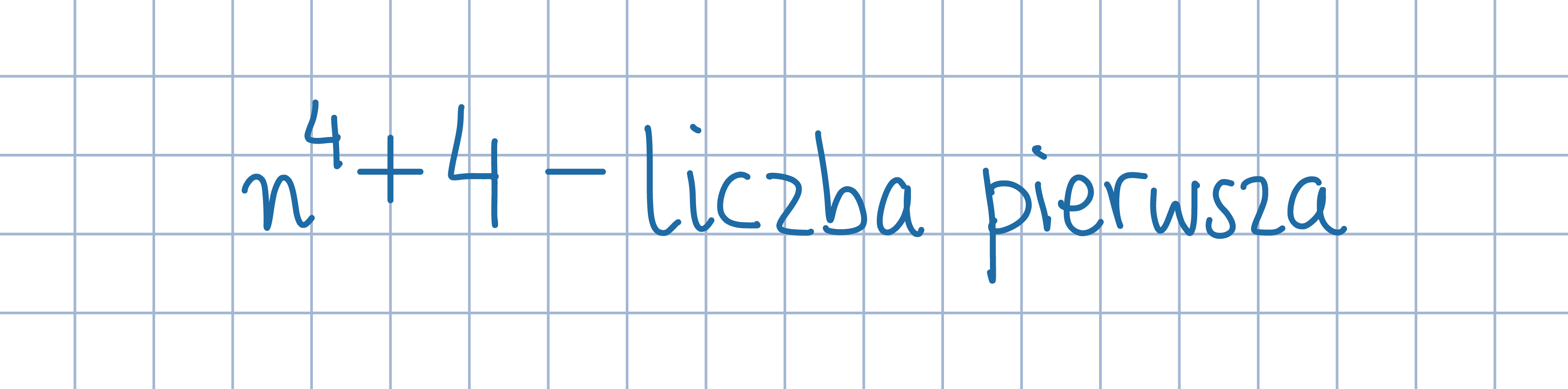 Odp.: n=1 jest jedyną liczbą spełniającą warunki zadania.
Odp.: n=1 jest jedyną liczbą spełniającą warunki zadania.

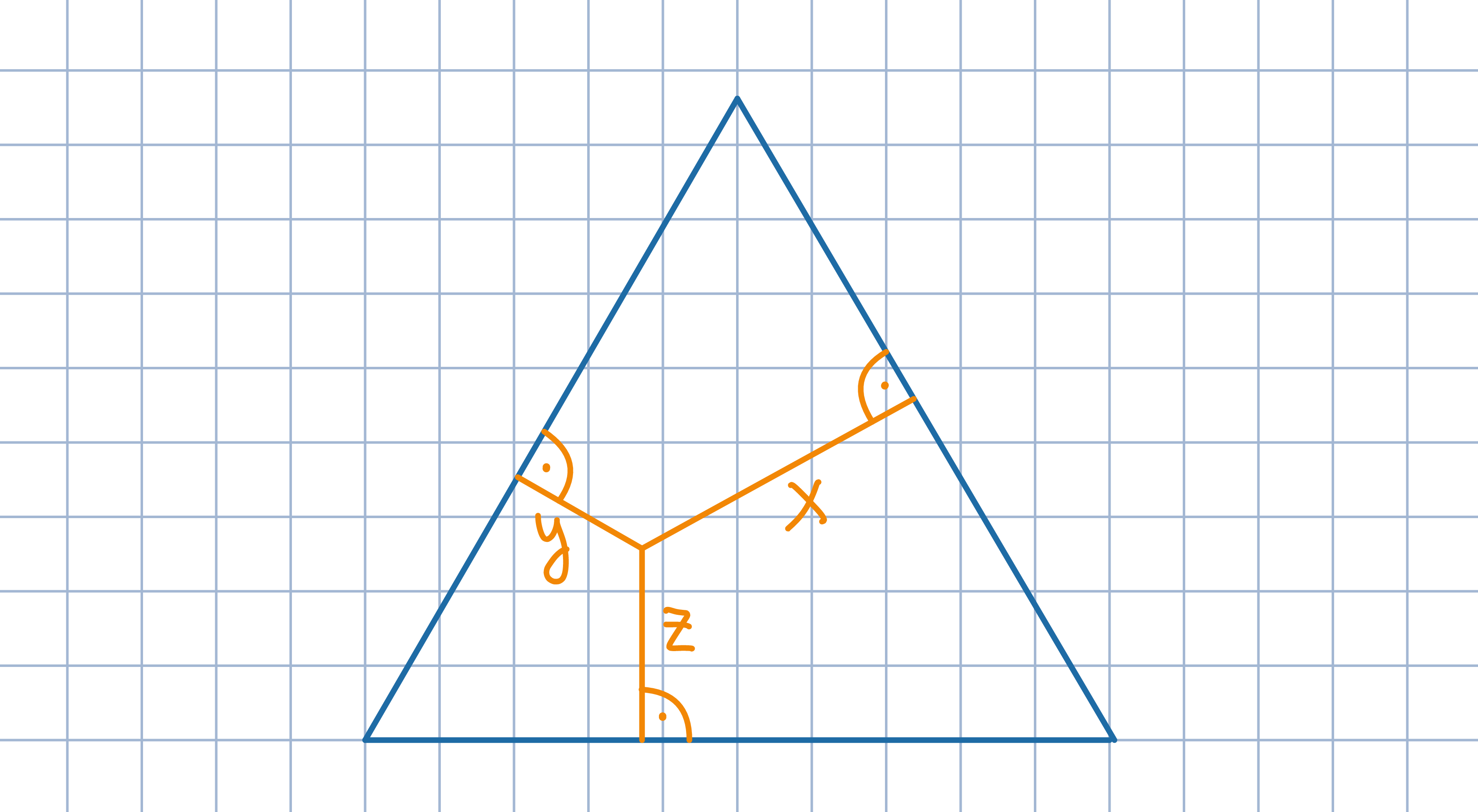 Łącząc wybrany punkt z wierzchołkami trójkąta
równobocznego, rozcinamy wyjściowy trójkąt na trzy mniejsze trójkąty. Porównaj sumę pól uzyskanych trzech trójkątów z polem danego trójkąta równobocznego.
Łącząc wybrany punkt z wierzchołkami trójkąta
równobocznego, rozcinamy wyjściowy trójkąt na trzy mniejsze trójkąty. Porównaj sumę pól uzyskanych trzech trójkątów z polem danego trójkąta równobocznego.

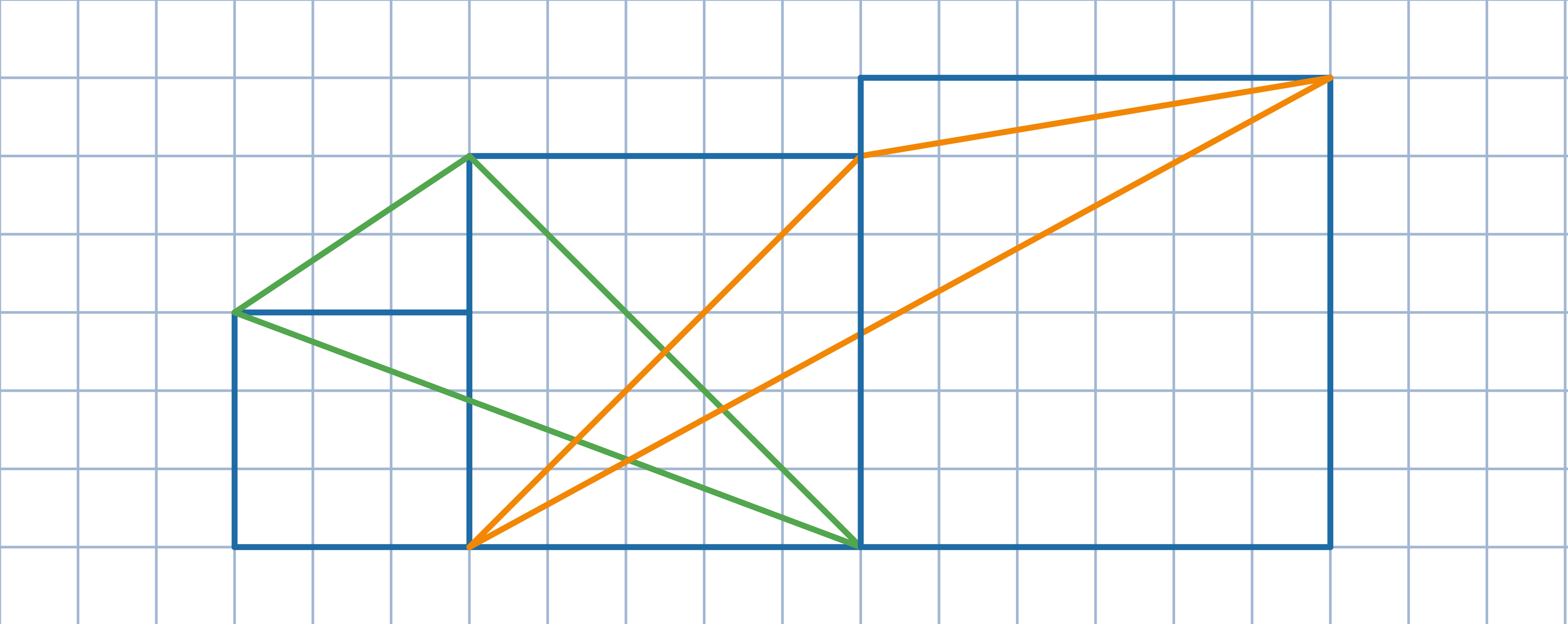
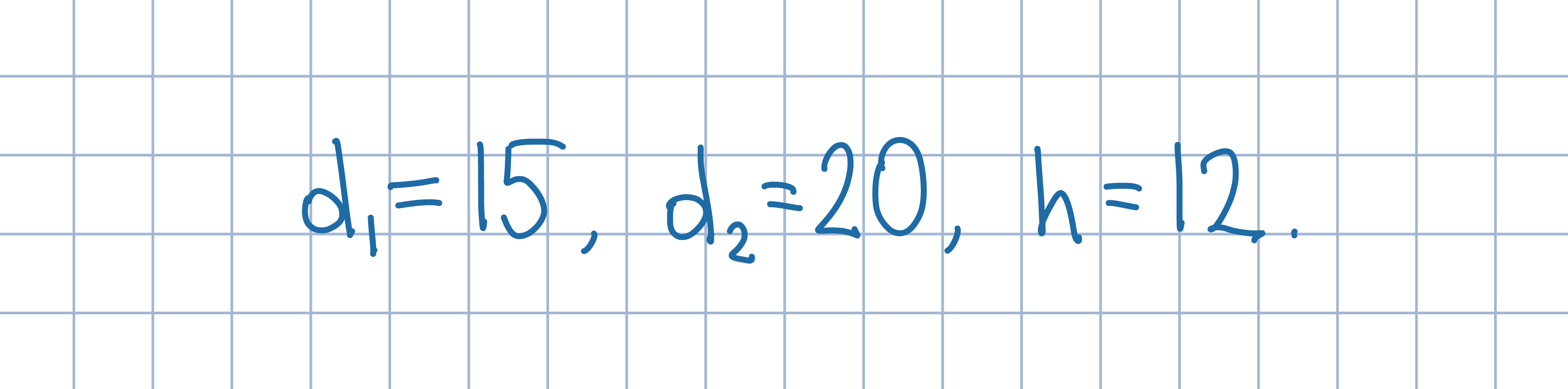 Odp:. 150 lub 42.
Odp:. 150 lub 42.Przedłuż dolną podstawę o długość górnej podstawy. Zauważ, że czworokąt, którego przeciwległymi bokami są zielone odcinki jest równoległobokiem.
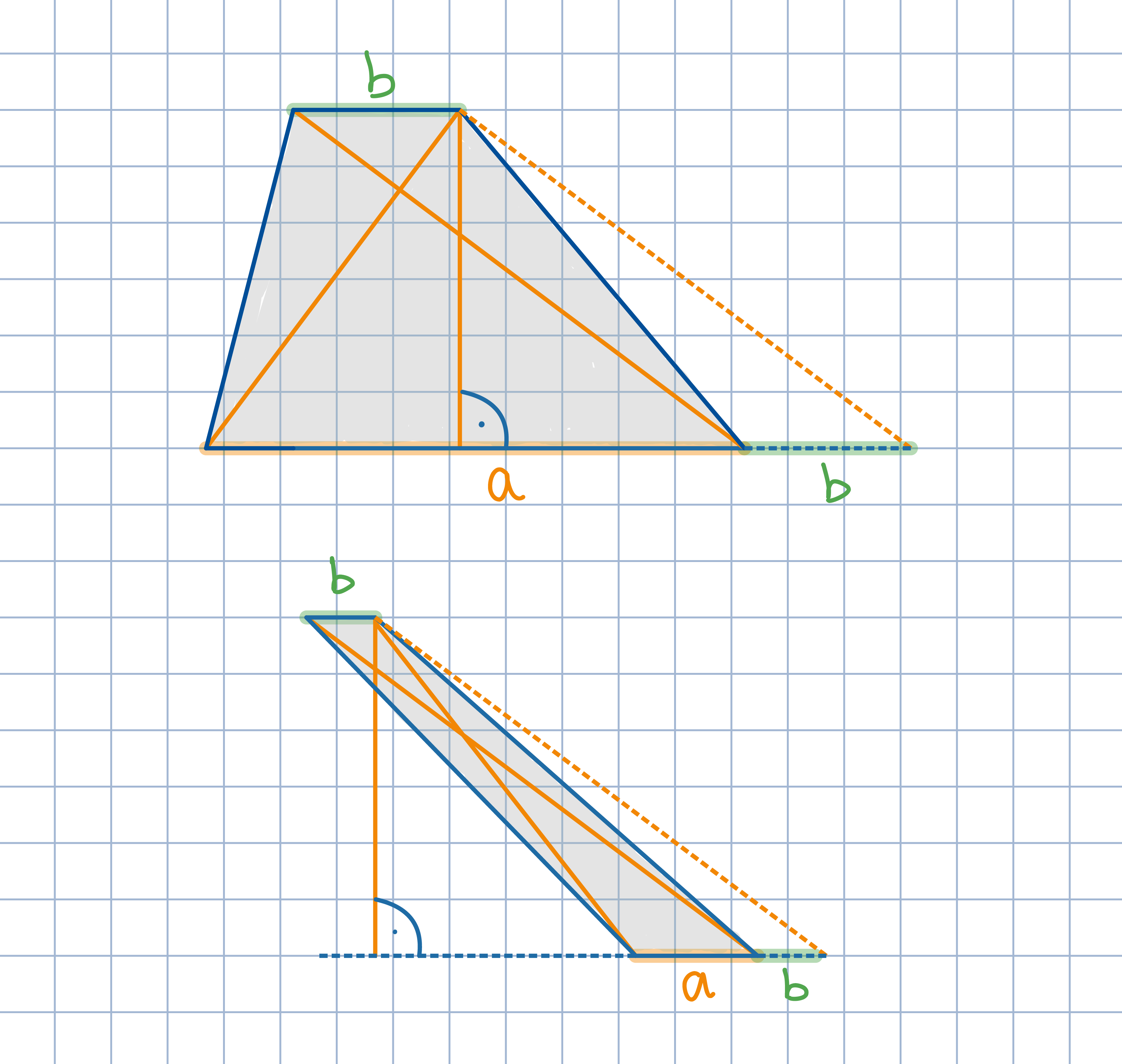
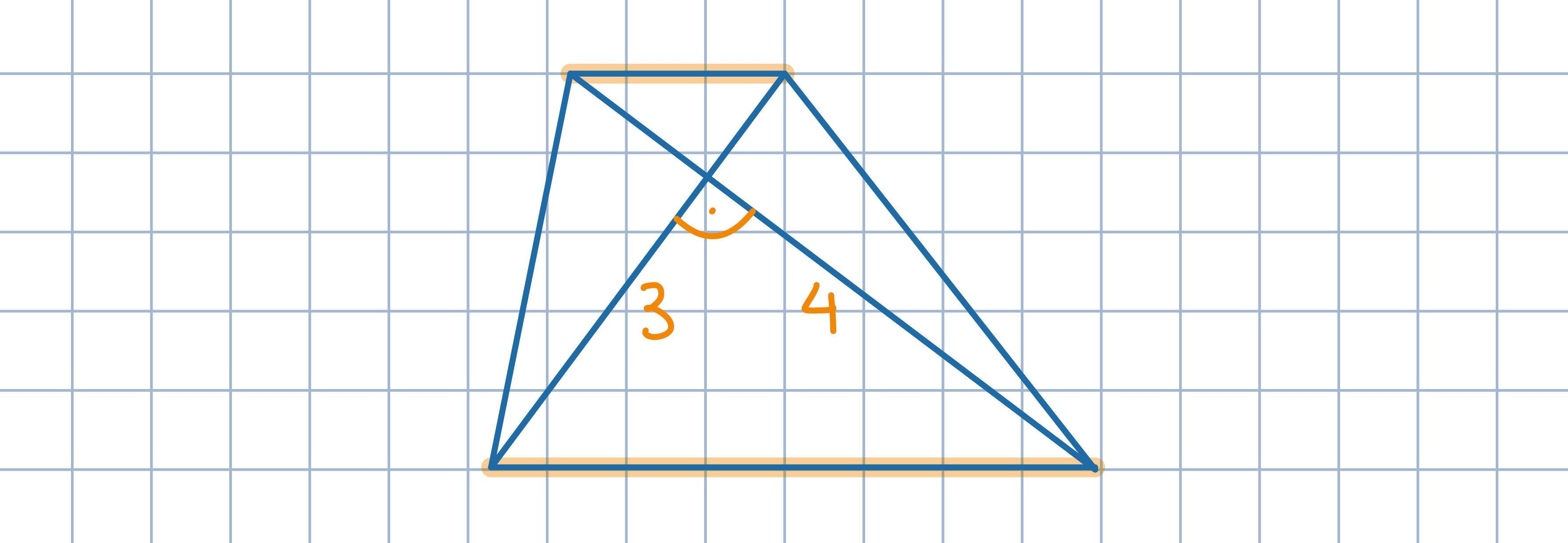 Odp:. 5.
Odp:. 5.Przedłuż dolną podstawę o długość górnej podstawy. Zauważ, że czworokąt, którego przeciwległymi bokami są pomarańczowe odcinki jest równoległobokiem.
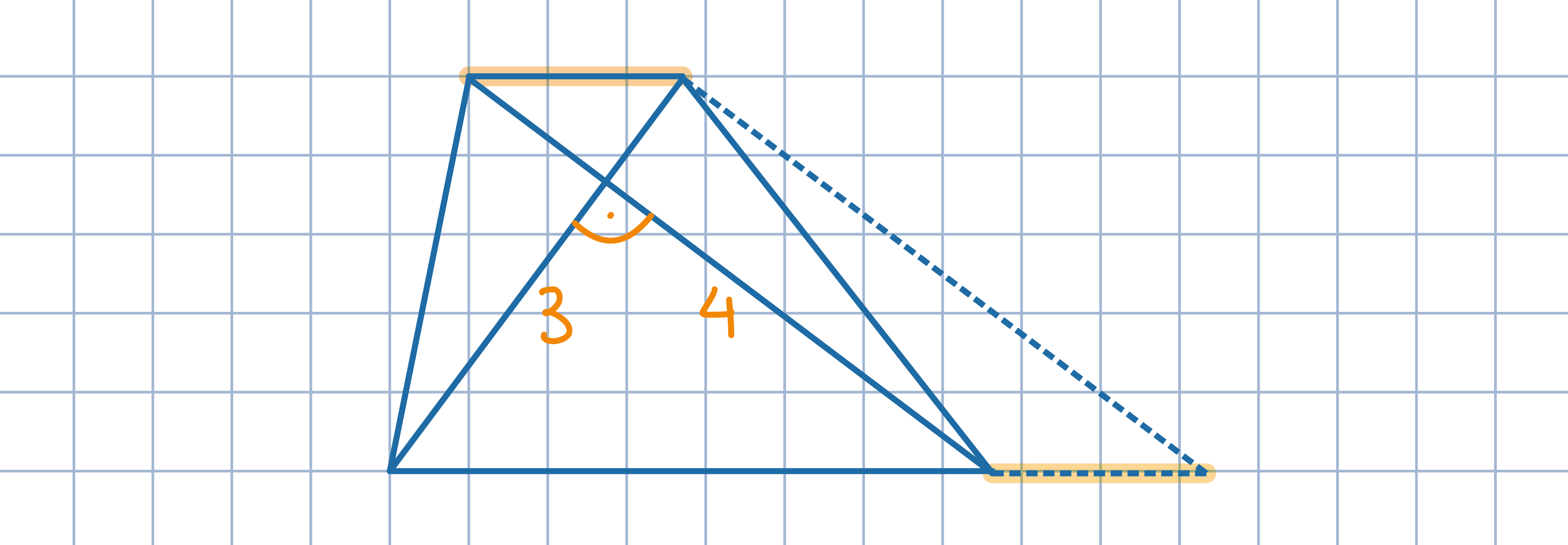
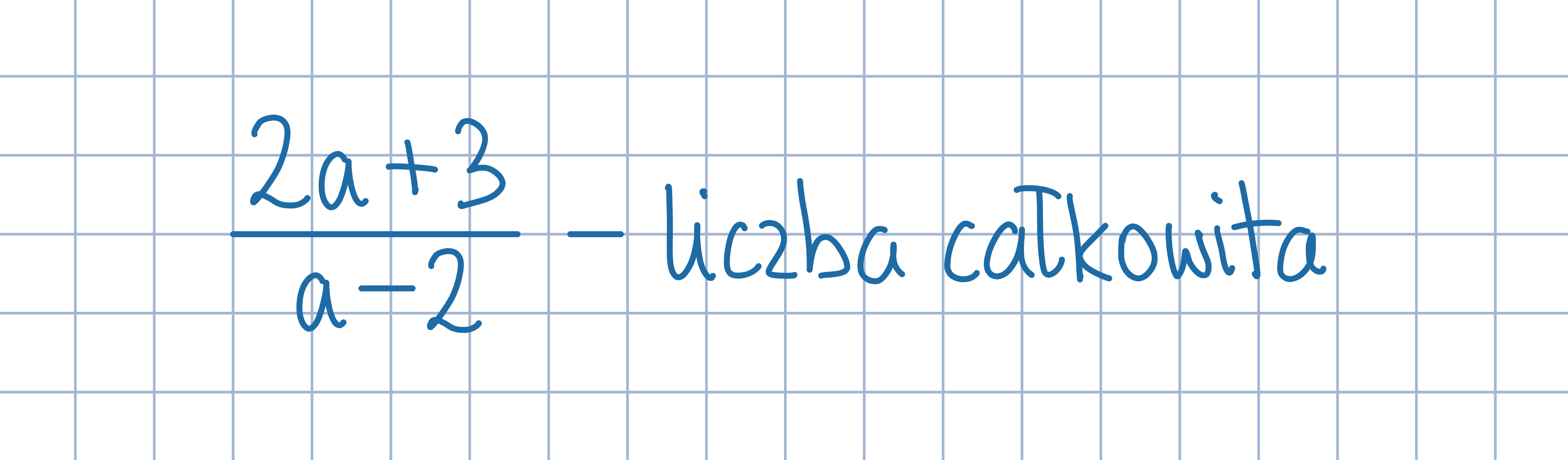 Odp:. a równa się –5, 1, 3 lub 9.
Odp:. a równa się –5, 1, 3 lub 9.
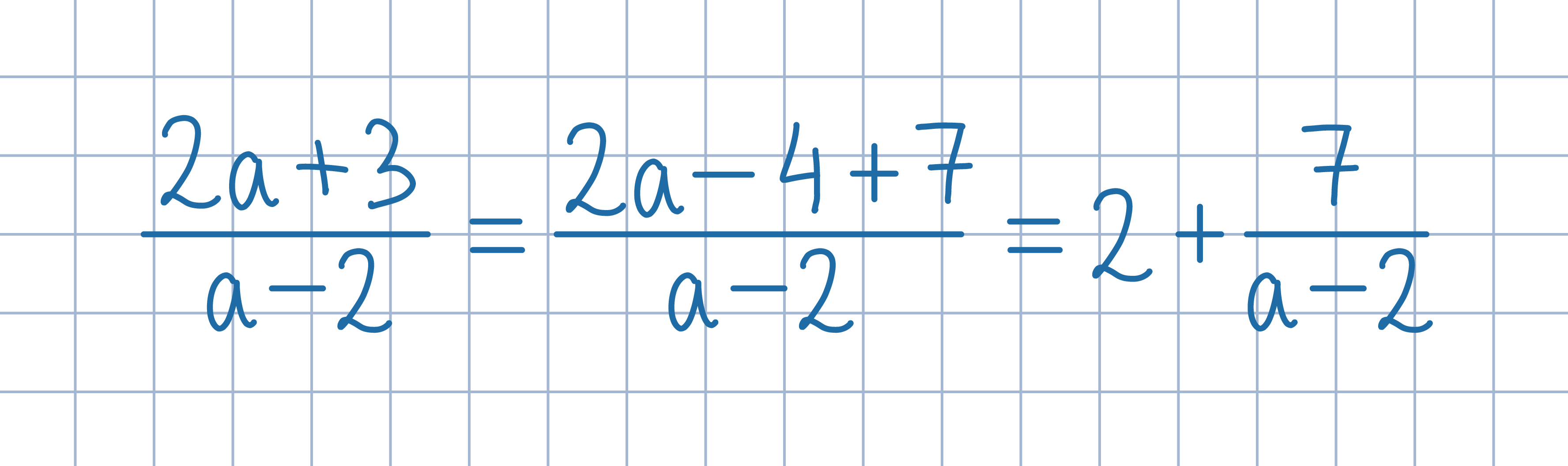
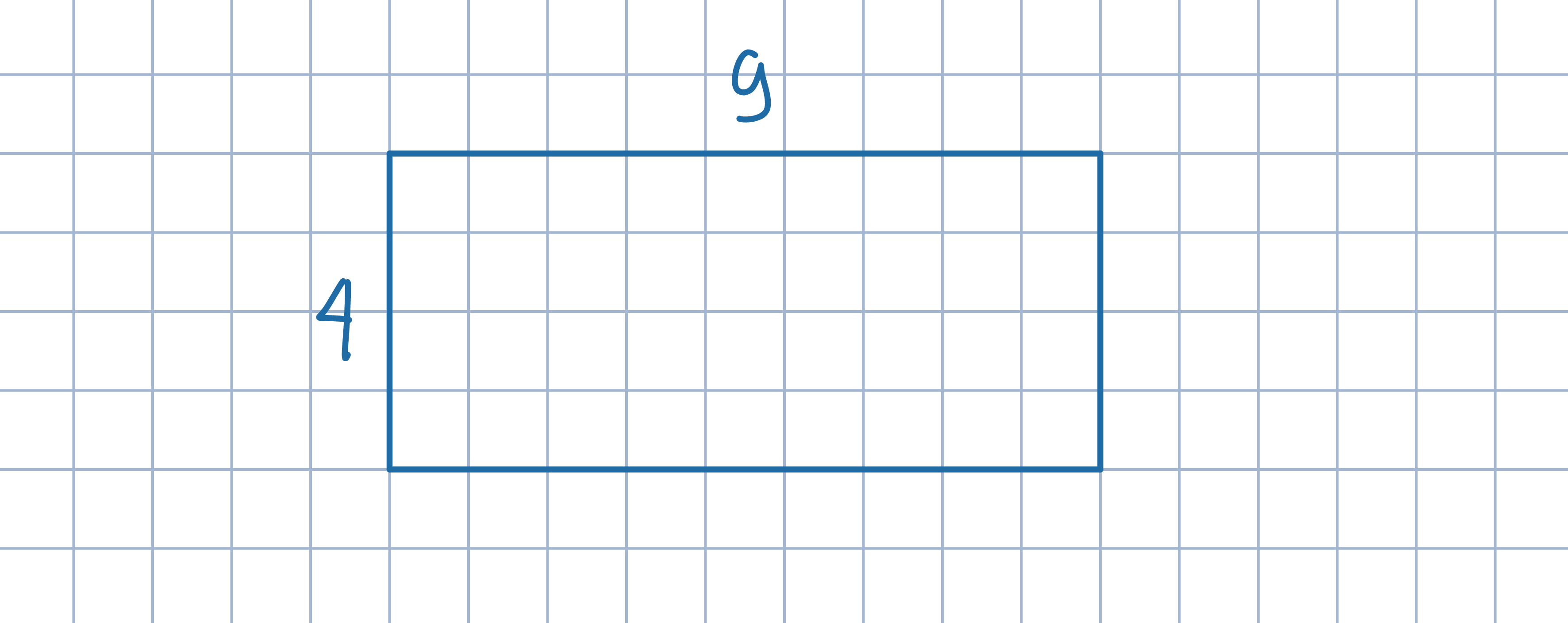



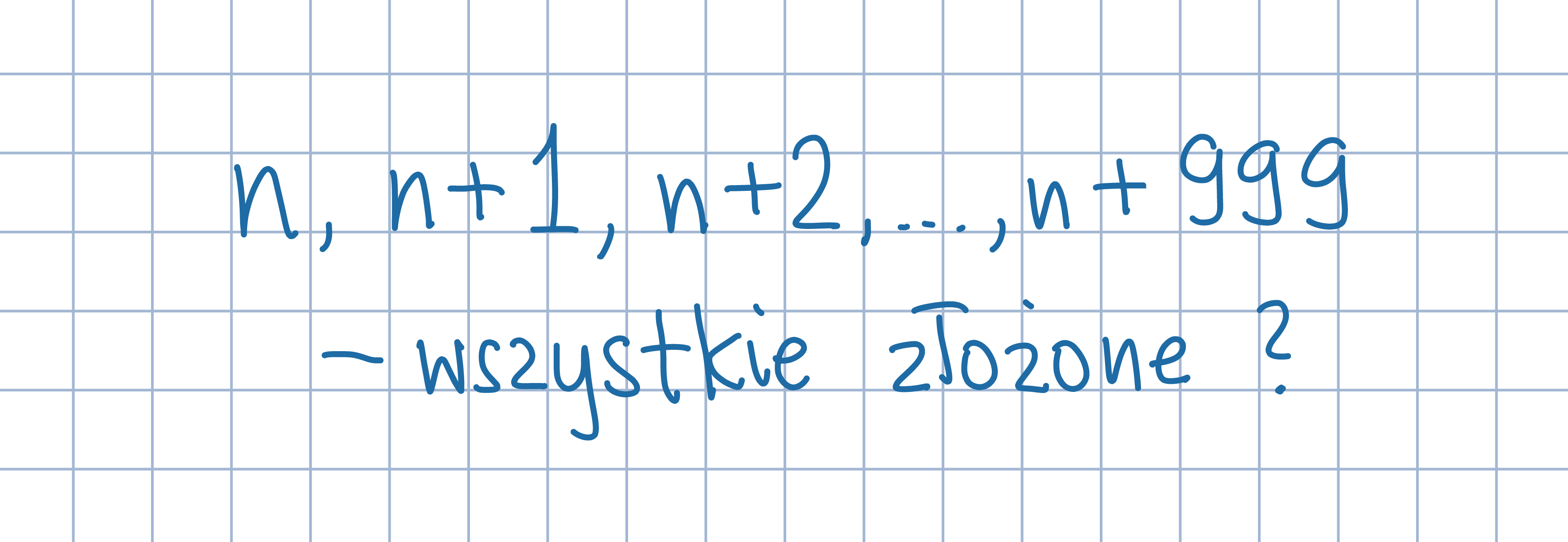 Tak, takie liczby istnieją, na przykład:
Tak, takie liczby istnieją, na przykład:1001!+2, 1001!+3, 1001!+4, ..., 1001!+1001.
Uwaga: Symbol n! oznacza iloczyn wszystkich liczb naturalnych od 1 do n.
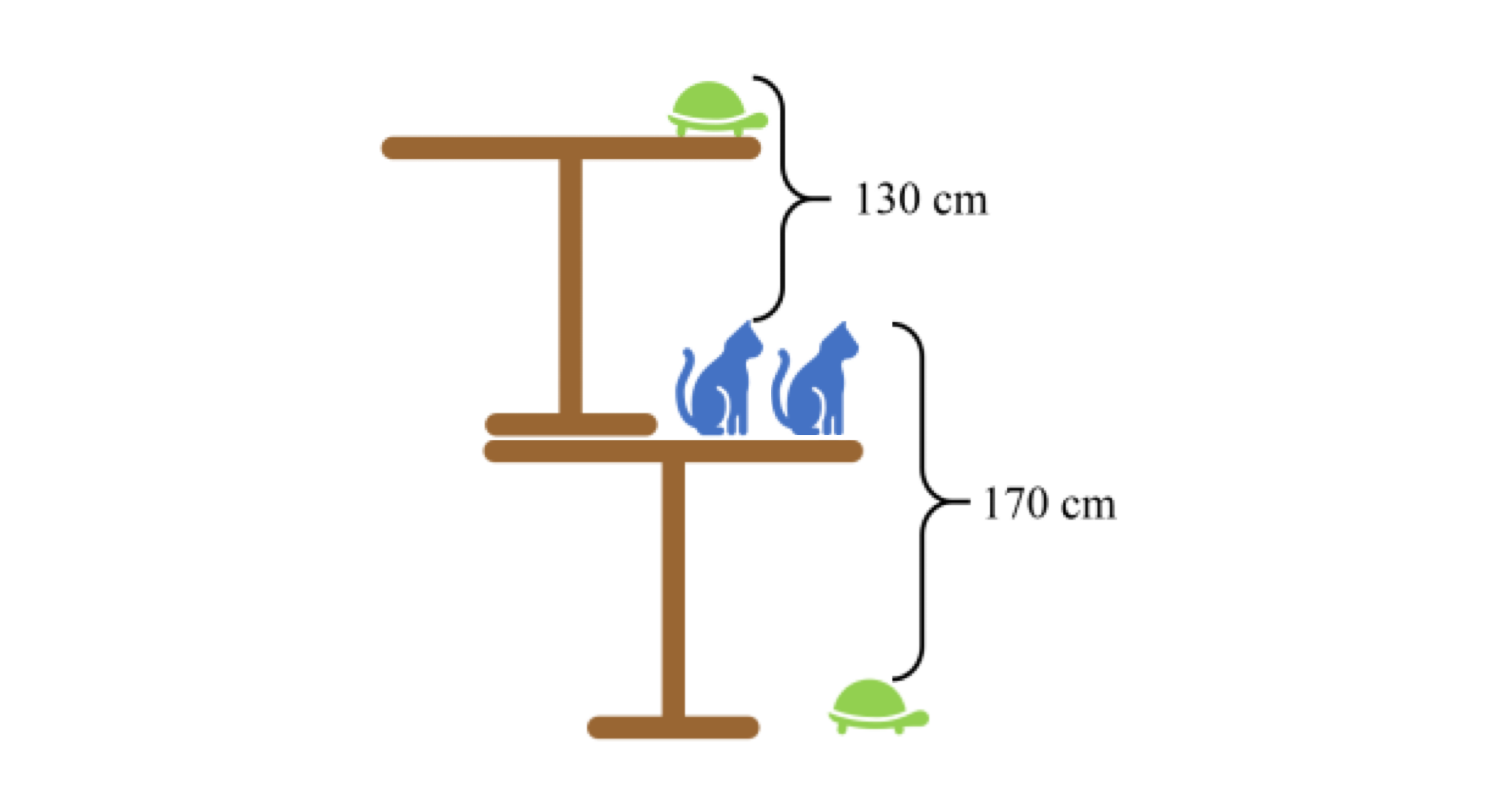
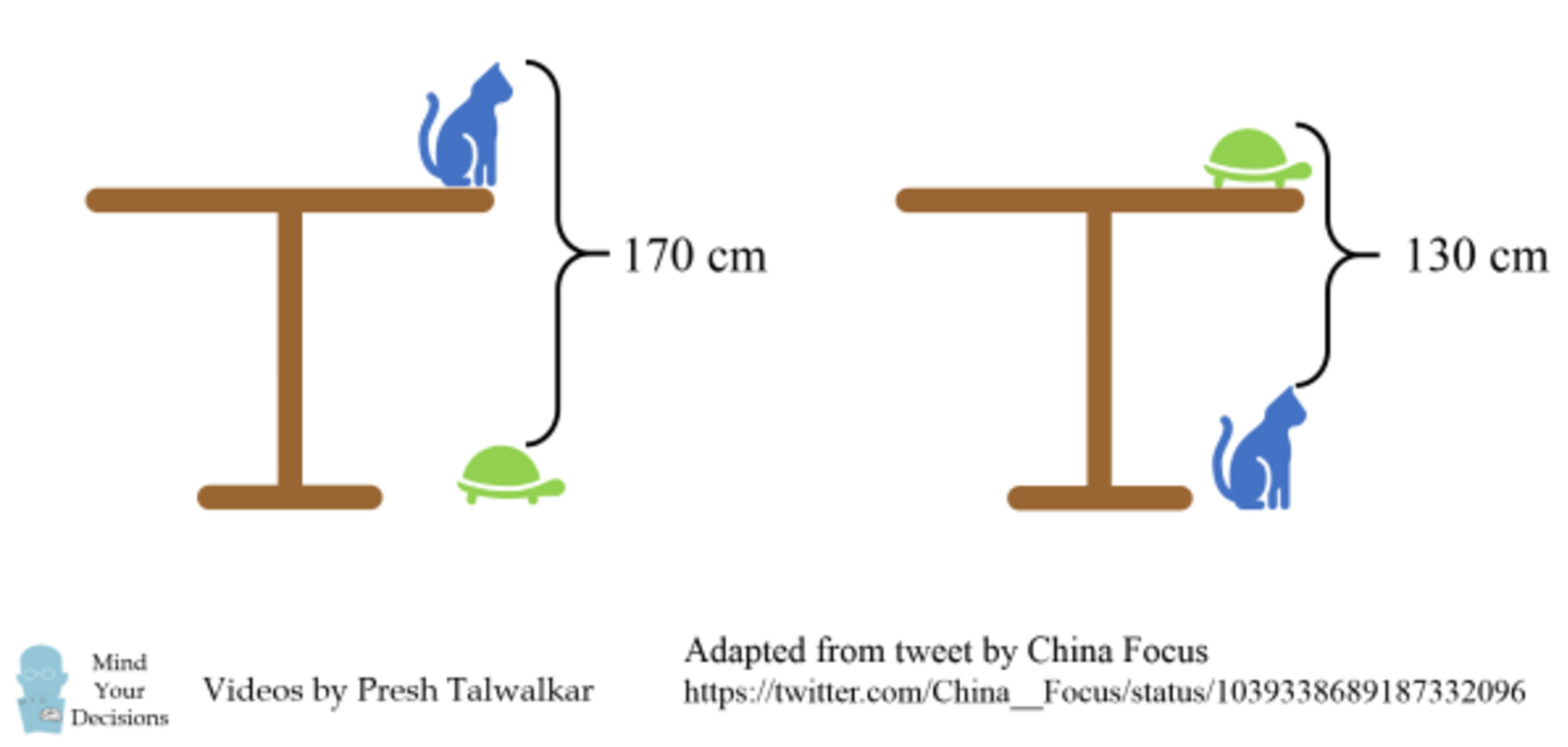 Odp.: 150 cm.
Odp.: 150 cm.Źródło: Mind Your Decisions, Presh Talwalker
 Tak, istnieje! Takim trójkątem jest na przykład trójkąt prostokątny
o przyprostokątnych długości 1 oraz 2.
Tak, istnieje! Takim trójkątem jest na przykład trójkąt prostokątny
o przyprostokątnych długości 1 oraz 2.
Najbliższe zajęcia
dla uczniów liceum oraz klas 7-8 szkoły podstawowej
zainteresowanych matematyką












